
【题目】小明随机调查了若干市民租用公共自行车的骑车时间t(单位:分),将获得的数据分成四组,绘制了如图统计图,请根据图中信息,解答下列问题:
(1)这次被调查的总人数是多少?
(2)试求表示A组的扇形圆心角的度数,并补全条形统计图.
(3)如果骑自行车的平均速度为12km/h,请估算,在租用公共自行车的市民中,骑车路程不超过6km的人数所占的百分比.
科目:初中数学 来源: 题型:
【题目】为加强中小学生安全教育,某校组织了“防溺水”知识竞赛,对表现优异的班级进行奖励,学校购买了若干副乒乓球拍和羽毛球拍,购买2副乒乓球拍和1副羽毛球拍共需116元;购买3副乒乓球拍和2副羽毛球拍共需204元.
(1)求购买1副乒乓球拍和1副羽毛球拍各需多少元;
(2)若学校购买乒乓球拍和羽毛球拍共30幅,且支出不超过1480元,则最多能够购买多少副羽毛球拍?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y= ![]() 的图象经过点(﹣1,﹣2
的图象经过点(﹣1,﹣2 ![]() ),点A是该图象第一象限分支上的动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点P,连结BP.
),点A是该图象第一象限分支上的动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点P,连结BP.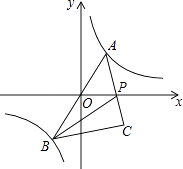
(1)k的值为 .
(2)在点A运动过程中,当BP平分∠ABC时,点C的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是矩形ABCD的对角线,⊙O是△ABC的内切圆,现将矩形ABCD按如图所示的方式折叠,使点D与点O重合,折痕为FG.点F,G分别在边AD,BC上,连结OG,DG.若OG⊥DG,且⊙O的半径长为1,则下列结论不成立的是( ) 
A.CD+DF=4
B.CD﹣DF=2 ![]() ﹣3
﹣3
C.BC+AB=2 ![]() +4
+4
D.BC﹣AB=2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景
已知在△ABC中,AB边上的动点D由A向B运动(与A,B不重合),点E与点D同时出发,由点C沿BC的延长线方向运动(E不与C重合),连接DE交AC于点F,点H是线段AF上一点.
(1)初步尝试
如图1,若△ABC是等边三角形,DH⊥AC,且点D,E的运动速度相等.
求证:HF=AH+CF.
小五同学发现可以由以下两种思路解决此问题:
思路一:过点D作DG∥BC,交AC于点G,先证GH=AH,再证GF=CF,从而证得结论成立;
思路二:过点E作EM⊥AC,交AC的延长线于点M,先证CM=AH,再证HF=MF,从而证得结论成立.
请你任选一种思路,完整地书写本小题的证明过程(如用两种方法作答,则以第一种方法评分);
(2)类比探究
如图2,若在△ABC中,∠ABC=90°,∠ADH=∠BAC=30°,且D,E的运动速度之比是 ![]() :1,求
:1,求 ![]() 的值;
的值;
(3)延伸拓展
如图3,若在△ABC中,AB=AC,∠ADH=∠BAC=36°,记 ![]() =m,且点D,E运动速度相等,试用含m的代数式表示
=m,且点D,E运动速度相等,试用含m的代数式表示 ![]() (直接写出结果,不必写解答过程).
(直接写出结果,不必写解答过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课本的作业题中有这样一道题:把一张顶角为36°的等腰三角形纸片剪两刀,分成3张小纸片,使每张小纸片都是等腰三角形,你能办到吗?请画示意图说明剪法. 我们有多少种剪法,图1是其中的一种方法: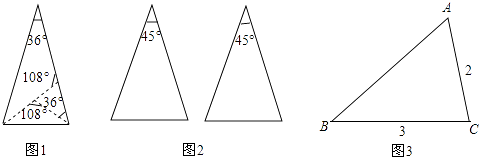
定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线.
(1)请你在图2中用两种不同的方法画出顶角为45°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数;(若两种方法分得的三角形成3对全等三角形,则视为同一种)
(2)△ABC中,∠B=30°,AD和DE是△ABC的三分线,点D在BC边上,点E在AC边上,且AD=BD,DE=CE,设∠C=x°,试画出示意图,并求出x所有可能的值;
(3)如图3,△ABC中,AC=2,BC=3,∠C=2∠B,请画出△ABC的三分线,并求出三分线的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com