
【题目】问题背景
已知在△ABC中,AB边上的动点D由A向B运动(与A,B不重合),点E与点D同时出发,由点C沿BC的延长线方向运动(E不与C重合),连接DE交AC于点F,点H是线段AF上一点.
(1)初步尝试
如图1,若△ABC是等边三角形,DH⊥AC,且点D,E的运动速度相等.
求证:HF=AH+CF.
小五同学发现可以由以下两种思路解决此问题:
思路一:过点D作DG∥BC,交AC于点G,先证GH=AH,再证GF=CF,从而证得结论成立;
思路二:过点E作EM⊥AC,交AC的延长线于点M,先证CM=AH,再证HF=MF,从而证得结论成立.
请你任选一种思路,完整地书写本小题的证明过程(如用两种方法作答,则以第一种方法评分);
(2)类比探究
如图2,若在△ABC中,∠ABC=90°,∠ADH=∠BAC=30°,且D,E的运动速度之比是 ![]() :1,求
:1,求 ![]() 的值;
的值;
(3)延伸拓展
如图3,若在△ABC中,AB=AC,∠ADH=∠BAC=36°,记 ![]() =m,且点D,E运动速度相等,试用含m的代数式表示
=m,且点D,E运动速度相等,试用含m的代数式表示 ![]() (直接写出结果,不必写解答过程).
(直接写出结果,不必写解答过程).
【答案】
(1)
证明(选择思路一):过点D作DG∥BC,交AC于点G,如图1所示:
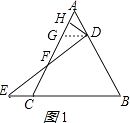
则∠ADG=∠B,∠AGD=∠ACB,
∵△ABC是等边三角形,
∴∠A=∠B=∠ACB=60°,
∴∠ADG=∠AGD=∠A,
∴△ADG是等边三角形,
∴GD=AD=CE,
∵DH⊥AC,
∴GH=AH,
∵DG∥BC,
∴∠GDF=∠CEF,∠DGF=∠ECF,
在△GDF和△CEF中,
 ,
,
∴△GDF≌△CEF(ASA),
∴GF=CF,
∴GH+GF=AH+CF,
即HF=AH+CF
(2)
解:过点D作DG∥BC,交AC于点G,如图2所示:
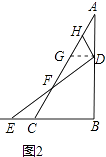
则∠ADG=∠B=90°,
∵∠BAC=∠ADH=30°,
∴∠HGD=∠HDG=60°,
∴AH=GH=GD,AD= ![]() GD,
GD,
根据题意得:AD= ![]() CE,
CE,
∴GD=CE,
∵DG∥BC,
∴∠GDF=∠CEF,∠DGF=∠ECF,
在△GDF和△CEF中,
 ,
,
∴△GDF≌△CEF(ASA),
∴GF=CF,
∴GH+GF=AH+CF,
即HF=AH+CF,
∴ ![]() =2;
=2;
(3)
解: ![]() ,理由如下:
,理由如下:
过点D作DG∥BC,交AC于点G,如图3所示:
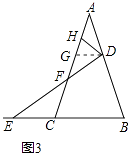
则∠ADG=∠B,∠AGD=∠ACB,
∵AB=AC,∠BAC=36°,
∴∠ACB=∠B=∠ADG=∠AGD=72°,
∵∠ADH=∠BAC=36°,
∴AH=DH,∠DHG=72°=∠AGD,
∴DG=DH=AH,△ADG∽△ABC,△ADG∽△DGH,
∴ ![]() =m,
=m, ![]() =m,
=m,
∴△DGH∽△ABC,
∴ ![]() =m,
=m,
∴ ![]() =m,
=m,
∵DG∥BC,
∴△DFG∽△EFC,
∴ ![]() =m,
=m,
∴ ![]() =m,
=m,
即 ![]() =m,
=m,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)过点D作DG∥BC,交AC于点G,先证明△ADG是等边三角形,得出GD=AD=CE,再证明GH=AH,由ASA证明△GDF≌△CEF,得出GF=CF,即可得出结论;(2)过点D作DG∥BC,交AC于点G,先证出AH=GH=GD,AD= ![]() GD,由题意AD=
GD,由题意AD= ![]() CE,得出GD=CE,再证明△GDF≌△CEF,得出GF=CF,即可得出结论;(3)过点D作DG∥BC,交AC于点G,先证出 DG=DH=AH,再证明△ADG∽△ABC,△ADG∽△DGH,△DGH∽△ABC,得出
CE,得出GD=CE,再证明△GDF≌△CEF,得出GF=CF,即可得出结论;(3)过点D作DG∥BC,交AC于点G,先证出 DG=DH=AH,再证明△ADG∽△ABC,△ADG∽△DGH,△DGH∽△ABC,得出 ![]() =m,
=m, ![]() =m,△DGH∽△ABC,得出
=m,△DGH∽△ABC,得出 ![]() =m,
=m, ![]() =m,证明△DFG∽△EFC,得出
=m,证明△DFG∽△EFC,得出 ![]() =m,
=m, ![]() =m,
=m, ![]() =
= ![]() ,即可得出结果.
,即可得出结果.
【考点精析】解答此题的关键在于理解相似三角形的应用的相关知识,掌握测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.


科目:初中数学 来源: 题型:
【题目】在如图的正方形网格中,每一个小正方形的边长为1.格点三角形ABC(顶点是网格线交点的三角形)的顶点A、C的坐标分别是(﹣4,6),(﹣1,4).
(1)请在图中的网格平面内建立平面直角坐标系;
(2)请画出△ABC关于x轴对称的△A1B1C1;
(3)请在y轴上求作一点P,使△PB1C的周长最小,并写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM,ON交于A,B两点,如果∠APB绕点P旋转时始终满足OAOB=OP2 , 我们就把∠APB叫做∠MON的智慧角.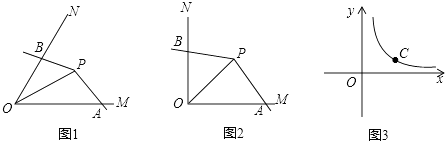
(1)如图2,已知∠MON=90°,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM,ON交于A,B两点,且∠APB=135°.求证:∠APB是∠MON的智慧角.
(2)如图1,已知∠MON=α(0°<α<90°),OP=2.若∠APB是∠MON的智慧角,连结AB,用含α的式子分别表示∠APB的度数和△AOB的面积.
(3)如图3,C是函数y= ![]() (x>0)图象上的一个动点,过C的直线CD分别交x轴和y轴于A,B两点,且满足BC=2CA,请求出∠AOB的智慧角∠APB的顶点P的坐标.
(x>0)图象上的一个动点,过C的直线CD分别交x轴和y轴于A,B两点,且满足BC=2CA,请求出∠AOB的智慧角∠APB的顶点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明随机调查了若干市民租用公共自行车的骑车时间t(单位:分),将获得的数据分成四组,绘制了如图统计图,请根据图中信息,解答下列问题:
(1)这次被调查的总人数是多少?
(2)试求表示A组的扇形圆心角的度数,并补全条形统计图.
(3)如果骑自行车的平均速度为12km/h,请估算,在租用公共自行车的市民中,骑车路程不超过6km的人数所占的百分比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线C1:y=a1x2+b1x+c1和C2:y=a2x2+b2x+c2都经过原点,顶点分别为A,B,与x轴的另一交点分别为M,N,如果点A与点B,点M与点N都关于原点O成中心对称,则称抛物线C1和C2为姐妹抛物线,请你写出一对姐妹抛物线C1和C2 , 使四边形ANBM恰好是矩形,你所写的一对抛物线解析式是和 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,设点P(1,t)在反比例函数y= ![]() 的图象上,过点P作直线l与x轴平行,点Q在直线l上,满足QP=OP.若反比例函数y=
的图象上,过点P作直线l与x轴平行,点Q在直线l上,满足QP=OP.若反比例函数y= ![]() 的图象经过点Q,则k= .
的图象经过点Q,则k= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的顶点A在第一象限,AB∥x轴,AD∥y轴,且对角线的交点与原点O重合.在边AB从小于AD到大于AD的变化过程中,若矩形ABCD的周长始终保持不变,则经过动点A的反比例函数y= ![]() (k≠0)中k的值的变化情况是( )
(k≠0)中k的值的变化情况是( ) 
A.一直增大
B.一直减小
C.先增大后减小
D.先减小后增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,汽车在东西向的公路l上行驶,途中A,B,C,D四个十字路口都有红绿灯.AB之间的距离为800米,BC为1000米,CD为1400米,且l上各路口的红绿灯设置为:同时亮红灯或同时亮绿灯,每次红(绿)灯亮的时间相同,红灯亮的时间与绿灯亮的时间也相同.若绿灯刚亮时,甲汽车从A路口以每小时30千米的速度沿l向东行驶,同时乙汽车从D路口以相同的速度沿l向西行驶,这两辆汽车通过四个路口时都没有遇到红灯,则每次绿灯亮的时间可能设置为( ) 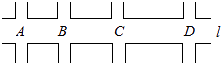
A.50秒
B.45秒
C.40秒
D.35秒
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=3,BC=2,点D是边AB上的动点,过点D作DE∥BC,交边AC于点E,点Q是线段DE上的点,且QE=2DQ,连接BQ并延长,交边AC于点P.设BD=x,AP=y. 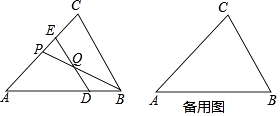
(1)求y关于x的函数解析式及定义域;
(2)当△PQE是等腰三角形时,求BD的长;
(3)连接CQ,当∠CQB和∠CBD互补时,求x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com