
【题目】计算:
(1)(﹣2)2﹣( ![]() )﹣1+20170
)﹣1+20170
(2)(1+ ![]() )÷
)÷ ![]() .
.
【答案】
(1)解:(﹣2)2﹣( ![]() )﹣1+20170
)﹣1+20170
=4﹣2+1
=3;
(2)解:(1+ ![]() )÷
)÷ ![]()
= ![]()
= ![]()
=x﹣2.
【解析】(1)根据负整数指数幂、零指数幂可以解答本题;(2)根据分式的加法和除法可以解答本题.
【考点精析】本题主要考查了分式的混合运算和零指数幂法则的相关知识点,需要掌握运算的顺序:第一级运算是加法和减法;第二级运算是乘法和除法;第三级运算是乘方.如果一个式子里含有几级运算,那么先做第三级运算,再作第二级运算,最后再做第一级运算;如果有括号先做括号里面的运算.如顺口溜:"先三后二再做一,有了括号先做里."当有多层括号时,先算括号内的运算,从里向外{[(?)]};零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数)才能正确解答此题.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=AC,tan∠B=2,BC=4,D为BC边的中点,点E在BC边的延长线上,且CE=BC,连接AE,F为线段AE的中点 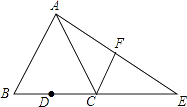
(1)求线段CF的长;
(2)求∠CAE的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课本上,同学们已经探究过“经过已知直线外一点作这条直线的垂线“的尺规作图过程:
已知:直线l和l外一点P
求作:直线l的垂线,使它经过点P.
作法:如图:⑴在直线l上任取两点A、B;
⑵分别以点A、B为圆心,AP,BP长为半径画弧,两弧相交于点Q;
⑶作直线PQ.
参考以上材料作图的方法,解决以下问题:
(1)以上材料作图的依据是:
(2)已知,直线l和l外一点P,
求作:⊙P,使它与直线l相切.(尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC与BD交于点O,过点O作BD的垂线分别交AD,BC于E,F两点.若AC=2 ![]() ,∠AEO=120°,则FC的长度为( )
,∠AEO=120°,则FC的长度为( ) 
A.1
B.2
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,设反比例函数的解析式为y= ![]() (k>0).
(k>0). 
(1)若该反比例函数与正比例函数y=2x的图象有一个交点的纵坐标为2,求k的值;
(2)若该反比例函数与过点M(﹣2,0)的直线l:y=kx+b的图象交于A,B两点,如图所示,当△ABO的面积为 ![]() 时,求直线l的解析式.
时,求直线l的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,菱形ABCD中,AB=5cm,动点P从点B出发,沿折线BC﹣CD﹣DA运动到点A停止,动点Q从点A出发,沿线段AB运动到点B停止,它们运动的速度相同,设点P出发xs时,△BPQ的面积为ycm2 , 已知y与x之间的函数关系如图②所示,其中OM,MN为线段,曲线NK为抛物线的一部分,请根据图中的信息,解答下列问题: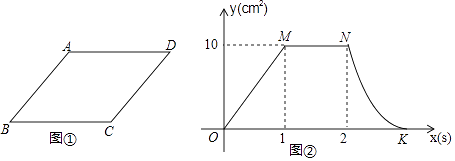
(1)当1<x<2时,△BPQ的面积(填“变”或“不变”);
(2)分别求出线段OM,曲线NK所对应的函数表达式;
(3)当x为何值时,△BPQ的面积是5cm2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市东坡实验中学准备开展“阳光体育活动”,决定开设足球、篮球、乒乓球、羽毛球、排球等球类活动,为了了解学生对这五项活动的喜爱情况,随机调查了m名学生(每名学生必选且只能选择这五项活动中的一种).
根据以上统计图提供的信息,请解答下列问题:
(1)m= , n= .
(2)补全上图中的条形统计图.
(3)若全校共有2000名学生,请求出该校约有多少名学生喜爱打乒乓球.
(4)在抽查的m名学生中,有小薇、小燕、小红、小梅等10名学生喜欢羽毛球活动,学校打算从小薇、小燕、小红、小梅这4名女生中,选取2名参加全市中学生女子羽毛球比赛,请用列表法或画树状图法,求同时选中小红、小燕的概率.(解答过程中,可将小薇、小燕、小红、小梅分别用字母A、B、C、D代表)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明用棋子摆放图形来研究数的规律.图1中棋子围成三角形,其棵数3,6,9,12,…称为三角形数.类似地,图2中的4,8,12,16,…称为正方形数.下列数中既是三角形数又是正方形数的是( )
A.2010
B.2012
C.2014
D.2016
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市计划在“十周年”庆典当天开展购物抽奖活动,凡当天在该超市购物的顾客,均有一次抽奖的机会,抽奖规则如下:将如图所示的圆形转盘平均分成四个扇形,分别标上1,2,3,4四个数字,抽奖者连续转动转盘两次,当每次转盘停止后指针所指扇形内的数为每次所得的数(若指针指在分界线时重转);当两次所得数字之和为8时,返现金20元;当两次所得数字之和为7时,返现金15元;当两次所得数字之和为6时返现金10元. 
(1)试用树状图或列表的方法表示出一次抽奖所有可能出现的结果;
(2)某顾客参加一次抽奖,能获得返还现金的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com