
����Ŀ���ۺ���̽��
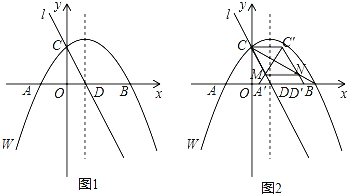
��ͼ1����ƽ��ֱ������ϵxOy�У�������W�ĺ�������ʽΪy=��![]() x2+
x2+![]() x+4��������W��x�ύ��A��B���㣨��B�ڵ�A���Ҳ࣬��y�ύ�ڵ�C�����ĶԳ�����x�ύ�ڵ�D��ֱ��l����C��D���㣮
x+4��������W��x�ύ��A��B���㣨��B�ڵ�A���Ҳ࣬��y�ύ�ڵ�C�����ĶԳ�����x�ύ�ڵ�D��ֱ��l����C��D���㣮
(1)��A��B��������꼰ֱ��l�ĺ�������ʽ��
(2)��������W��x������ƽ�Ƶõ�������W������������W���ĶԳ�����ֱ��l���ڵ�F������ACFΪֱ��������ʱ�����F�����꣬��ֱ��д����ʱ������W���ĺ�������ʽ��
(3)��ͼ2������AC��CB������ACD��x������ƽ��m����λ��0��m��5�����õ���A��C��D������A��C��ֱ��l�ڵ�M��C��D����CB�ڵ�N������CC�䣬MN�����ı���CMNC����������ú�m�Ĵ���ʽ��ʾ����
���𰸡���1����A����Ϊ����3��0������B������Ϊ��7��0����y=��2x+4��(2) ��F������Ϊ��5����6����y=��![]() x2+
x2+![]() x��(3) �ı���CMNC������Ϊ
x��(3) �ı���CMNC������Ϊ![]() m2.
m2.
��������
���������ߵĽ���ʽ����y��0����������������.���������ߵĽ���ʽ�ɷֱ����C��D��������꣬���ô���ϵ�����������ֱ�ߵı���ʽ.
�������⣬���ýǵĵ�����ϵ���Եõ���1����3�������õ�tan��1��tan��3���������Ǻ����ļ��㷽���г���ʽ������һ�κ����Ľ���ʽ���![]() ������Ϊ��xF����2xF��4���������߶εij��ȴ����ʽ���������F�����꣬�ٸ���ƽ�Ƶķ������w���ı���ʽ.
������Ϊ��xF����2xF��4���������߶εij��ȴ����ʽ���������F�����꣬�ٸ���ƽ�Ƶķ������w���ı���ʽ.
����ƽ�ƣ����Եõ���C�䣬A�䣬D�������꣬�ٸ��ݴ���ϵ�������Եõ�ֱ��A��C�䣬BC��C��D���Ľ���ʽ�����ݽ���ļ��㷽���з����������õ�M��N�����꣬����ƽ�ƵĶ����ƽ���ı��εĶ����֪�ı���CMNC����ƽ���ı��Σ��ٸ���ƽ���ı�������ļ��㷽�����Եõ�ƽ���ı���CMNC�������.
��1����y��0ʱ����![]() x2��
x2��![]() ��4��0�����x1����3��x2��7��
��4��0�����x1����3��x2��7��
���A��������3��0������B��������7��0����
����![]() ��
��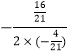
��������w�ĶԳ���Ϊֱ��x��2��
���D������2��0����
��x��0ʱ��y��4��
���C��������0��4����
��ֱ��l�ı���ʽΪy��kx��b��
![]()
���![]()
��ֱ��l�Ľ���ʽΪy����2x��4��
(2)��������w����ƽ�ƣ�ֻ��һ���������Ҫ��
����FAC��90������ͼ.
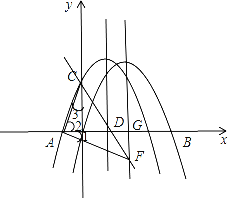
��ʱ������w���ĶԳ�����x��Ľ���ΪG��
�ߡ�1����2��90����2����3��90�㣬
���1����3��
��tan��1��tan��3��
��![]() =
=![]() �����F��������xF����2xF��4����
�����F��������xF����2xF��4����
��![]() ��
��![]() �����xF��5����2xF��4����6��
�����xF��5����2xF��4����6��
���F������Ϊ��5����6������ʱ������w���ĺ�������ʽΪy����![]() x2��
x2��![]() x��
x��
(3)��ƽ�ƿɵã���C������A������D��������ֱ�ΪC�䣨m��4����A�䣨��3��m��0����D�䣨2��m��0����CC����x�ᣬC��D����CD��
���ô���ϵ�������
ֱ��A��C���ı���ʽΪy��![]() x��4��
x��4��![]() m��
m��
ֱ��BC�ı���ʽΪy����![]() x��4��
x��4��
ֱ��C��D���ı���ʽΪy����2x��2m��4��
�ֱ�ⷽ����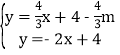 ��
��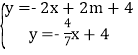
���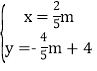 ��
��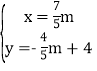
���M��������![]() m����
m����![]() m��4������N��������
m��4������N��������![]() m����
m����![]() m��4����
m��4����
��yM��yN
��MN��x�ᣬ
��CC����x�ᣬ
��CC����MN��
��C��D����CD��
���ı���CMNC����ƽ���ı��Σ�
��S��m[4������![]() m��4��]
m��4��]
��![]() m2
m2



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳���һ����������ת����Բ��ת�̣���ͼ�����涨���˿���100Ԫ���Ͽ��Ի��һ��ת��ת�̵Ļ��ᣬ��ת��ֹͣʱ��ָ��������һ������ͻ����Ӧ�Ľ�Ʒ��ָ��ָ���������εĽ���ʱ������ָ���ұߵ����Σ����±��ǻ�����е�һ��ͳ�����ݣ�
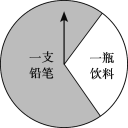
ת��ת�̵Ĵ���n | 100 | 150 | 200 | 500 | 800 | 1000 |
������Ǧ�����Ĵ���m | 68 | 111 | 136 | 345 | 546 | 701 |
������Ǧ������Ƶ�� ���������С�������λ�� | 0.68 | 0.74 | 0.68 | 0.69 | 0.68 | 0.70 |
��1��ת����ת��һ�Σ����Ǧ�ʵĸ���ԼΪ_______�����������С�����һλ��
��2��Ǧ��ÿֻ0.5Ԫ������ÿƿ3Ԫ����ͳ�Ƹ��̳�ÿ��Լ��4000���˿Ͳμӳ齱����������̳�ÿ����Ҫ֧���Ľ�Ʒ���ã�
��3���ڣ�2���������£����̳����ÿ��֧���Ľ�Ʒ���ÿ�����3000Ԫ���ң���ת���ϡ�һƿ���ϡ������Բ�Ľ�Ӧ����Ϊ______�ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڶ��κ���y����x2��bx��c�У�����y���Ա���x�IJ��ֶ�Ӧֵ���±���
x | ���� | ��2 | 0 | 3 | 4 | ���� |
y | ���� | ��7 | m | n | ��7 | ���� |
��m��n�Ĵ�С��ϵΪ( )
A. m��n B. m��n C. m��n D. ��ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���������ABCD�����ڲ���ÿ����������²�������ÿ����ĺᡢ�����궼����ͬһ��ʵ��a�����õ��ĵ�������ƽ��m����λ��������ƽ��n����λ��m��0��n��0�����õ�������A'B'C'D'�����ڲ��ĵ㣬���е�A��B�Ķ�Ӧ��ֱ�ΪA'��B'����֪������ABCD�ڲ���һ����F��������������õ��Ķ�Ӧ��F'���F�غϣ����F�������ǣ�������
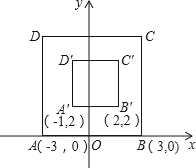
A. ��1��4�� B. ��1��5�� C. ����1��4�� D. ��4��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪AB�ǡ�O��ֱ������CD��AB��H����CD�ӳ�����һ��E����O�����߽�AB���ӳ�����F���е�ΪG������AG��CD��K��
��1����ͼ1����֤��KE=GE��
��2����ͼ2������CABG������FGB=![]() ��ACH����֤��CA��FE��
��ACH����֤��CA��FE��
��3����ͼ3���ڣ�2���������£�����CG��AB�ڵ�N����sinE=![]() ��AK=
��AK=![]() ����CN�ij���
����CN�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У���A=��B=90�㣬P���߶�AB�ϵ�һ�����㣮
��1����AD=2��BC=6��AB=8������A��D��PΪ���������������B��C��PΪ��������������ƣ���AP�ij���
��2����AD=a��BC=b��AB=m����a��b��m����ʲô��ϵʱ��һ�����ڵ�Pʹ��ADP�ס�BPC����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������y=![]() ��kΪ��������k��0����ͼ����A��1��3����B��3��m����
��kΪ��������k��0����ͼ����A��1��3����B��3��m����
��1�����������Ľ���ʽ��B������ꣻ
��2����x������һ��P��ʹPA+PB��ֵ��С�������������ĵ�P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�����ϱ������ϵIJ���������A�㴦��ú���B�ڵ�A����ƫ��30�����������Ϻ���30���ﵽ��C��ʱ����ú���B��C��ı�ƫ��15��������ô����B��˺��ߵ���������ǣ��������С�������λ�����ο����ݣ�![]() ���� ��
���� ��
A. 4.64���� B. 5.49���� C. 6.12���� D. 6.21����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB��AC����P��D�ֱ���BC��AC���ϵĵ㣬�ҡ�APD����B.
(1)��֤��AC��CD��CP��BP��
(2)��AB��10��BC��12����PD��ABʱ����BP�ij���
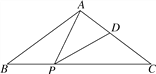
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com