
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���������ABCD�����ڲ���ÿ����������²�������ÿ����ĺᡢ�����궼����ͬһ��ʵ��a�����õ��ĵ�������ƽ��m����λ��������ƽ��n����λ��m��0��n��0�����õ�������A'B'C'D'�����ڲ��ĵ㣬���е�A��B�Ķ�Ӧ��ֱ�ΪA'��B'����֪������ABCD�ڲ���һ����F��������������õ��Ķ�Ӧ��F'���F�غϣ����F�������ǣ�������
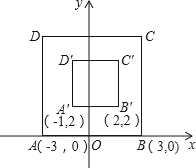
A. ��1��4�� B. ��1��5�� C. ����1��4�� D. ��4��1��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ұ��ݰ˺��������滮��������ͨ��������Ҫ��ɲ����������ɸ�����2017��12��6�տ�ͨ��Ӫ���������ɶ��г�����ʱ����14Сʱ����Ϊ3.5Сʱ����������ǿ��Լ�ӳɶ����������������Σ���ͼ�������ң�����A���ڳɶ���վ������B����ƫ��30���ķ��������4000�ף���ǿ�ң�����C���ڳɶ���վ��ƫ��60���ķ��������3000�ף�������������ǿ�ҵľ���Ϊ��������
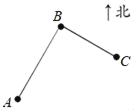
A. 6000�� B. 5000�� C. 4000�� D. 2000��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ѧУ�������Ա�����б��CD��һ����AB�ĸ߶ȣ��������ڵ�C���������B������Ϊ60����Ȼ�����¶�D�������B������Ϊ30������֪DE��EA��б��CD�ij���Ϊ30m��DE�ij�Ϊ15m������AB�ĸ߶���_____m��
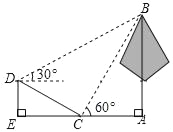
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
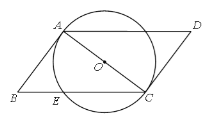
����Ŀ����ͼ��AC�ǡ�O��ֱ����AB���O�����ڵ�A���ı���ABCD��ƽ���ı��Σ�BC����O�ڵ�E��
��1��֤��ֱ��CD���O���У�
��2������O�İ뾶Ϊ5 cm����CE�ij�Ϊ8 cm����AB�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y1=��x+2��ͼ���뷴��������y2=![]() ��ͼ���ڵ�A����1��3����B��n����1����
��ͼ���ڵ�A����1��3����B��n����1����
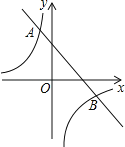
��1�����������Ľ���ʽ��
��2����y1��y2ʱ��ֱ��д��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y��ax2+2ax+c��a��0��c��0������x�ύ��A��B���㣨A��B��ࣩ����y�ύ�ڵ�C��A������Ϊ����3��0���������߶���ΪD����ACD�����Ϊ3��
��1������κ�������ʽ��
��2����P��m��n���������ߵ���������һ�㣬P����ԭ��ĶԳƵ�Q�ڵ�һ�����ڣ���QB2ȡ��Сֵʱ����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���̽��
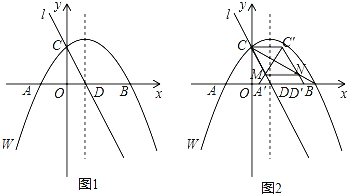
��ͼ1����ƽ��ֱ������ϵxOy�У�������W�ĺ�������ʽΪy=��![]() x2+
x2+![]() x+4��������W��x�ύ��A��B���㣨��B�ڵ�A���Ҳ࣬��y�ύ�ڵ�C�����ĶԳ�����x�ύ�ڵ�D��ֱ��l����C��D���㣮
x+4��������W��x�ύ��A��B���㣨��B�ڵ�A���Ҳ࣬��y�ύ�ڵ�C�����ĶԳ�����x�ύ�ڵ�D��ֱ��l����C��D���㣮
(1)��A��B��������꼰ֱ��l�ĺ�������ʽ��
(2)��������W��x������ƽ�Ƶõ�������W������������W���ĶԳ�����ֱ��l���ڵ�F������ACFΪֱ��������ʱ�����F�����꣬��ֱ��д����ʱ������W���ĺ�������ʽ��
(3)��ͼ2������AC��CB������ACD��x������ƽ��m����λ��0��m��5�����õ���A��C��D������A��C��ֱ��l�ڵ�M��C��D����CB�ڵ�N������CC�䣬MN�����ı���CMNC����������ú�m�Ĵ���ʽ��ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+c(a��0)��ͼ����ͼ��ʾ�������½���ͬʱ��������![]() ����
����![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD���ĸ�����ֱ��ڷ���������![]() ��
��![]() (x��0��0��m��n)��ͼ���ϣ��Խ���BD//y�ᣬ��BD��AC�ڵ�P����֪��B�ĺ�����Ϊ4��
(x��0��0��m��n)��ͼ���ϣ��Խ���BD//y�ᣬ��BD��AC�ڵ�P����֪��B�ĺ�����Ϊ4��
��1����m=4��n=20ʱ��
������P��������Ϊ2����ֱ��AB�ĺ�������ʽ��
������P��BD���е㣬���ж��ı���ABCD����״����˵�����ɣ�
��2���ı���ABCD�ܷ��Ϊ�����Σ����ܣ����ʱm��n֮���������ϵ�������ܣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com