【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示，则以下结论同时成立的是
A. 
B. 
C. 
D. 
口算题卡河北少年儿童出版社系列答案
A加金题 系列答案
全优测试卷系列答案科目：初中数学 来源： 题型：
【题目】类比、转化、从特殊到一般等思想方法在数学学习和研究中经常用到，如下是一个案例，请补充完整.
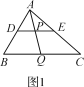
原题：如图1，在△ABC中，点D，E，Q分别在AB，AC，BC上，且DE∥BC，AQ交DE于点P，求证：
＝
.
(1)尝试探究：在图1中，由DP∥BQ，得△ADP___△ABQ(填“≌”或“∽”)，则＝___，同理可得＝
，从而＝；
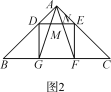
(2)类比延伸：如图2，在△ABC中，∠BAC＝90°，正方形DEFG的四个顶点在△ABC的边上，连接AG，AF分别交DE于M，N两点，若AB＝AC＝1，则MN的长为_____；
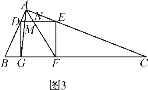
(3)拓展迁移：如图3，在△ABC中，∠BAC＝90°，正方形DEFG的四个顶点在△ABC的边上，连接AG，AF分别交DE于M，N两点，AB＜AC，求证：MN2＝DM·EN.
查看答案和解析>>
科目：初中数学 来源： 题型：
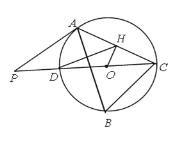
【题目】如图，△ABC内接于⊙O，∠B＝60°，CD是⊙O的直径，点P是CD延长线上的一点，且AP＝AC．
（1）求证：PA是⊙O的切线；
（2）若OH⊥AC，OH＝1，求DH的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
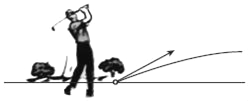
【题目】如图，以40m/s的速度将小球沿与地面成30°角的方向击出时，小球的飞行路线是一条抛物线．如果不考虑空气阻力，小球的飞行高度h（单位：m）与飞行时间t（单位：s）之间具有函数关系h＝20t﹣5t2．
（1）求小球飞行3s时的高度；
（2）问：小球的飞行高度能否达到22m？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
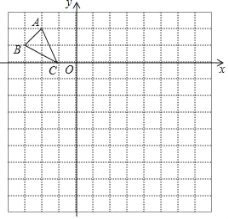
【题目】如图，在边长为1个单位长度的小正方形组成的12×12网格中建立平面直角坐标系，格点△ABC(顶点是网格线的交点)的坐标分别是A(﹣2，2)，B(﹣3，1)，C(﹣1，0)．
(1)将△ABC绕点O逆时针旋转90°得到△DEF，画出△DEF；
(2)以O为位似中心，将△ABC放大为原来的2倍，在网格内画出放大后的△A1B1C1，若P(x，y)为△ABC中的任意一点，这次变换后的对应点P1的坐标为 .
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，已知A(2,0)，B(1,－1)，将线段OA绕点O逆时针旋转，旋转角为
(0°<<135°).记点A的对应点为A1，若点A1与点B的距离为
，则为( ).
A. 30° B. 45° C. 60° D. 90°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小李的活鱼批发店以44元/公斤的价格从港口买进一批2000公斤的某品种活鱼，在运输过程中，有部分鱼未能存活，小李对运到的鱼进行随机抽查，结果如表一.由于市场调节，该品种活鱼的售价与日销售量之间有一定的变化规律，表二是近一段时间该批发店的销售记录.
(1)请估计运到的2000公斤鱼中活鱼的总重量；(直接写出答案)
(2)按此市场调节的观律，
①若该品种活鱼的售价定为52.5元/公斤，请估计日销售量，并说明理由；
②考虑到该批发店的储存条件，小李打算8天内卖完这批鱼(只卖活鱼)，且售价保持不变，求该批发店每日卖鱼可能达到的最大利润，并说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
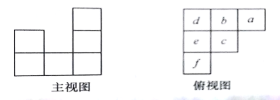
【题目】用小立方体搭一个几何体，使它的主视图和俯视图如图所示，俯视图中小正方形中字母表示在该位置小立方体的个数，请解答下列问题：
（1）求
的值；
（2）这个几何体最少有几个小立方体搭成，最多有几个小立方体搭成；
（3）当
时画出这个几何体的左视图.
查看答案和解析>>
科目：初中数学 来源： 题型：
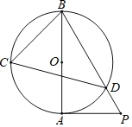
【题目】如图AB是⊙O的直径，PA与⊙O相切于点A，BP与⊙O相交于点D，C为⊙O上的一点，分别连接CB、CD，∠BCD＝60°．
(1)求∠ABD的度数；
(2)若AB＝6，求PD的长度．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
