
【题目】类比、转化、从特殊到一般等思想方法在数学学习和研究中经常用到,如下是一个案例,请补充完整.
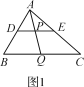
原题:如图1,在△ABC中,点D,E,Q分别在AB,AC,BC上,且DE∥BC,AQ交DE于点P,求证:![]() =
=![]() .
.
(1)尝试探究:在图1中,由DP∥BQ,得△ADP___△ABQ(填“≌”或“∽”),则![]() =___,同理可得
=___,同理可得![]() =
=![]() ,从而
,从而![]() =
=![]() ;
;
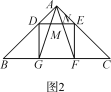
(2)类比延伸:如图2,在△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG,AF分别交DE于M,N两点,若AB=AC=1,则MN的长为_____;
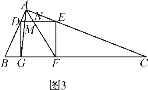
(3)拓展迁移:如图3,在△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG,AF分别交DE于M,N两点,AB<AC,求证:MN2=DM·EN.
【答案】(1)∽;![]() ;(2)
;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)可证明△ADP∽△ABQ,△ACQ∽△ADP,从而根据等比代换,得出![]()
(2)根据三角形的面积公式求出BC边上的高![]() ,根据△ADE∽△ABC,求出正方形DEFG的边长
,根据△ADE∽△ABC,求出正方形DEFG的边长![]() ,根据
,根据![]() 等于高之比,即可求出MN;
等于高之比,即可求出MN;
(3)可得出△BGD∽△EFC,则DGEF=CFBG;又由DG=GF=EF,得![]() ,再根据(1)
,再根据(1)![]() ,从而得出答案.
,从而得出答案.
(1)如图1,
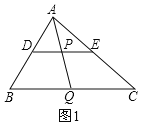
∵DP∥BQ,
∴△ADP∽△ABQ,
∴![]()
同理可得△ACQ∽△APE,
∴![]()
∴![]()
故答案为:∽;![]() ;
;
(2)如图2所示,
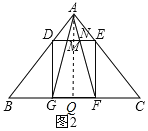
作AQ⊥BC于点Q.
∵BC边上的高![]()
且△ABC中,∠BAC=90°,正方形DEFG的四个顶点
∴DE=DG=GF=EF=BG=CF,
∴DE:BC=1:3,
又∵DE∥BC,
∴AD:AB=1:3,
∴![]()
∵DE边上的高为![]() ,
,![]()
∴![]()
∴MN=![]() .
.
(3)证明:
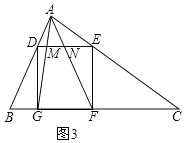
![]()
∵∠B+∠C=90°,∠CEF+∠C=90°,
∴∠B=∠CEF.
又∵∠BGD=∠EFC=90°,
∴△BGD∽△EFC.
∴![]() ,即DG·EF=CF·BG.
,即DG·EF=CF·BG.
又∵DG=GF=EF,∴GF2=CF·BG.
由(1)易得![]()
∴![]()
∴![]()
∵GF2=CF·BG,
∴MN2=DM·EN.


科目:初中数学 来源: 题型:
【题目】某校数学兴趣小组在探究如何求tan15°的值,经过自主思考、合作交流讨论,得到以下思路:
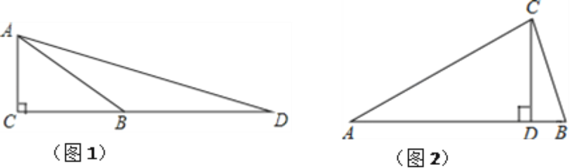
思路一 如图1,在Rt△ABC中,∠C=90°,∠ABC=30°,延长CB至点D,使BD=BA,连接AD.……
思路二 如图2,在顶角为30°的等腰三角形ABC中,AB=AC,若过点C作CD⊥AB于点D,则∠BCD=15°……
思路三 利用科普书上的有关公式:tan(α+β)=![]() ;
;
tan(α―β)=![]() ;…
;…
请解决下列问题(上述思路仅供参考).
(1)选择你喜欢的一种思路,完成解答过程,求出tan 15°的值(保留根号);
(2)试利用同样的方法,计算tan22.5°的值(保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为6的正六边形ABCDEF的中心与坐标原点O重合,AF∥x轴.将正六边形绕原点逆时针旋转n次,每次旋转60°,当n=2019时,顶点A的坐标为_____.
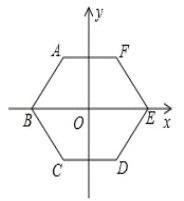
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系y=mx2+20x+n,其图象如图所示.
(1)m=_____,n=_____.
(2)销售单价为多少元时,该种商品每天的销售利润最大?最大利润为多少元?
(3)该种商品每天的销售利润不低于16元时,直接写出x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两个可以自由转动的均匀的转盘,甲转盘被分成3个面积相等
的扇形,乙转盘被分成4个面积相等的扇形,每一个扇形都标有相应的数字,同时转
动两个转盘,当转盘停止后,设甲转盘中指针所指区域内的数字为m,乙转盘中指针
所指区域内的数字为n(若指针指在边界线上时,重转一次,直到指针都指向一个区
域为止).

【1】请你用画树状图或列表格的方法求出|m+n|>1的概率
【2】直接写出点(m,n)落在函数y=- 图象上的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x1、x2是关于x的方程x2+2x+2k﹣4=0两个实数根,并且x1≠x2.
(1)求实数k的取值范围;
(2)若k为正整数,且该方程的根都是整数,求k的值;
(3)若|x1﹣x2|=6,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣5,1),B(﹣2,2),C(﹣1,4),请按下列要求画图:
(1)将△ABC先向右平移4个单位长度、再向下平移1个单位长度,得到△A1B1C1,画出△A1B1C1;
(2)画出与△ABC关于原点O成中心对称的△A2B2C2,并直接写出点A2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
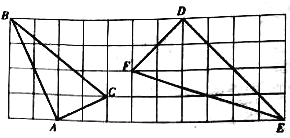
【题目】如图,在由边长均为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点(网格线的交点)上,请按要求完成下列各题.
(1)试证明△ABC是直角三角形;
(2)判断△ABC和△DEF是否相似,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com