
【题目】某校数学兴趣小组在探究如何求tan15°的值,经过自主思考、合作交流讨论,得到以下思路:
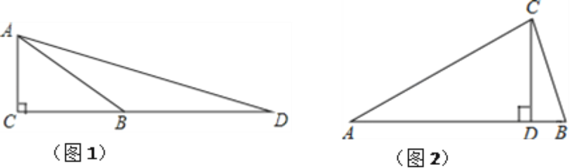
思路一 如图1,在Rt△ABC中,∠C=90°,∠ABC=30°,延长CB至点D,使BD=BA,连接AD.……
思路二 如图2,在顶角为30°的等腰三角形ABC中,AB=AC,若过点C作CD⊥AB于点D,则∠BCD=15°……
思路三 利用科普书上的有关公式:tan(α+β)=![]() ;
;
tan(α―β)=![]() ;…
;…
请解决下列问题(上述思路仅供参考).
(1)选择你喜欢的一种思路,完成解答过程,求出tan 15°的值(保留根号);
(2)试利用同样的方法,计算tan22.5°的值(保留根号).
【答案】(1)2-![]() ;(2)
;(2)![]() -1
-1
【解析】
(1)选择思路2,因为AB=AC,∠A=30°,CD⊥AB,可得CD=![]() AC,设CD=
AC,设CD=![]() AC=x,根据勾股定理可得AD=
AC=x,根据勾股定理可得AD=![]() x,所以BD=AB-AD=2x-
x,所以BD=AB-AD=2x-![]() x=(2-
x=(2-![]() )x,从而求解.
)x,从而求解.
(2)可设∠ABC=45°,因为AB=BD,可得∠D=22,5°,设AB=BD=![]() 。然后求出
。然后求出![]() 的值即可.
的值即可.
(1)思路2: 解:由已知AB=AC,
∵∠A=30°,CD⊥AB,∴CD=![]() AC=x,∠BCD=90°-
AC=x,∠BCD=90°-![]() (180°-30°)=15°,
(180°-30°)=15°,
则AD2=AC2-CD2=(2x)2-x2=3x2,∴AD=![]() x,
x,
∴BD=AB-AD=2x-![]() x=(2-
x=(2-![]() )x,
)x,
∴tan ∠BCD =tan15°=![]() =
=![]() =2-
=2-![]() .
.
(其它思路同样可以)
(2)在图1中,,设∠ABC=45°,AB=BD=![]() ,
,
∴∠D=![]() ∠ABC=22.5°,∵AB=
∠ABC=22.5°,∵AB=![]() ,∠ABC=45°,∴AC=BC=1,
,∠ABC=45°,∴AC=BC=1,
∴tan∠D=tan22.5°=![]() =
=![]() -1.
-1.


 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
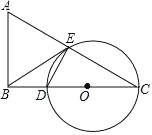
【题目】如图,在△ABC 中,∠ABC=90°,∠C=30°,AC 的垂直平分线交 BC 于点 D,交AC 于点 E.
(1)判断 BE 与△DCE 的外接圆⊙O 的位置关系,并说明理由;
(2)若 BE=![]() ,BD=1,求△DCE 的外接圆⊙O 的直径.
,BD=1,求△DCE 的外接圆⊙O 的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“爱我永州”中学生演讲比赛中,五位评委分别给甲、乙两位选手的评分如下:
甲:8、8、9、8、7乙:7、9、9、6、9
则下列说法中错误的是( )
A.甲、乙得分的平均数都是8
B.甲得分的众数是8,乙得分的众数是9
C.甲得分的中位数是9,乙得分的中位数是6
D.甲得分的方差比乙得分的方差小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.
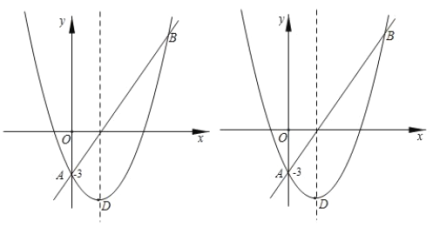
(1)求抛物线的解析式及顶点坐标;
(2)在![]() 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,∠BAD=90°,过C作CE⊥AD垂足为E,且∠EDC=∠BDC.
(1)求证:CE是⊙O的切线;
(2)若DE+CE=4,AB=6,求BD的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班七个兴趣小组人数分别为4,4,5,5,x,6,7,已知这组数据的平均数是5,则这组数据的众数和中位数分别是( )
A. 4,5 B. 4,4 C. 5,4 D. 5,5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校是乒乓球体育传统项目学校,为进一步推动该项目的开展,学校准备到体育用品店购买直拍球拍和横拍球拍若干副,并且每买一副球拍必须要买10个乒乓球,乒乓球的单价为2元/个,若购买20副直拍球拍和15副横拍球拍花费9000元;购买10副横拍球拍比购买5副直拍球拍多花费1600元.
(1)求两种球拍每副各多少元?
(2)若学校购买两种球拍共40副,且直拍球拍的数量不多于横拍球拍数量的3倍,请你给出一种费用最少的方案,并求出该方案所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=![]() ,O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE,CF.
,O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE,CF.
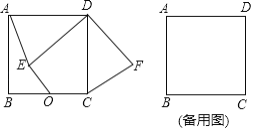
(1)求证:AE=CF;
(2)若A,E,O三点共线,连接OF,求线段OF的长.
(3)求线段OF长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
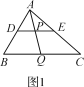
【题目】类比、转化、从特殊到一般等思想方法在数学学习和研究中经常用到,如下是一个案例,请补充完整.
原题:如图1,在△ABC中,点D,E,Q分别在AB,AC,BC上,且DE∥BC,AQ交DE于点P,求证:![]() =
=![]() .
.
(1)尝试探究:在图1中,由DP∥BQ,得△ADP___△ABQ(填“≌”或“∽”),则![]() =___,同理可得
=___,同理可得![]() =
=![]() ,从而
,从而![]() =
=![]() ;
;
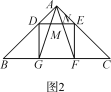
(2)类比延伸:如图2,在△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG,AF分别交DE于M,N两点,若AB=AC=1,则MN的长为_____;
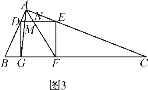
(3)拓展迁移:如图3,在△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG,AF分别交DE于M,N两点,AB<AC,求证:MN2=DM·EN.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com