
����Ŀ��ijѧУ��ƹ����������ͳ��ĿѧУ��Ϊ��һ���ƶ�����Ŀ�Ŀ�չ��ѧУ����������Ʒ�깺��ֱ�����ĺͺ����������ɸ�������ÿ��һ�����ı���Ҫ��10��ƹ����ƹ����ĵ���Ϊ2Ԫ/����������20��ֱ�����ĺ�15���������Ļ���9000Ԫ������10���������ıȹ���5��ֱ�����Ķ��1600Ԫ��
��1������������ÿ��������Ԫ��
��2����ѧУ�����������Ĺ�40������ֱ�����ĵ����������ں�������������3�����������һ�ַ������ٵķ�����������÷���������ã�
���𰸡���1��ֱ������ÿ��220Ԫ��������ÿ��260Ԫ����2������ֱ������30�������������10��ʱ���������٣�
��������
��1����ֱ������ÿ��xԪ���������е���ȹ�ϵ��20��ֱ�����ĵļ�Ǯ+15���������ĵļ�Ǯ��9000Ԫ��10���������ļ�Ǯ��5��ֱ�����ļ�Ǯ��1600Ԫ�����������鼴����⣻
��2���蹺��ֱ������m�������������г�����ʽ�ɵó�m��ȡֵ��Χ���ٸ��������г����ù���m��һ�κ�����������һ�κ��������ʽ��.
�⣺��1����ֱ������ÿ��xԪ��������ÿ��yԪ��������ã�
![]()
��ã�![]() ��
��
��ֱ������ÿ��220Ԫ��������ÿ��260Ԫ��
��2���蹺��ֱ������m�������������40-m������
������ã�m��3��40-m����
��ã�m��30��
����40����������ķ���Ϊw��
��w=��220+20��m+��260+20����40-m��
=-40m+11200��
��-40��0��
��w��m�����������
����m=30ʱ��wȡ��Сֵ����СֵΪ-40��30+11200=10000��Ԫ����
�𣺹���ֱ������30�������������10��ʱ���������٣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������������е�ÿ��С�����εı߳�����1��ÿ��С��Ķ��������㣮
��1����ͼ1���Ը��Ϊ���㻭һ�����Ϊ10�������Σ�
��2����ͼ2���Ը��Ϊ���㻭һ�������Σ�ʹ���������߳��ֱ�Ϊ2��![]() ��
��![]() ��
��
��3����ͼ3����A��B��C��С�����εĶ��㣬���ABC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪MB=ND����MBA=��NDC�������ĸ����������ж���ABM�ա�CDN�� ��

A.AM=CNB.AB=CD C.AM��CN D.��M=��N
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������mȡʲôʵ������A��m+1��2m��2������ֱ��l�ϣ�����B��a��b����ֱ��l�ϵĶ��㣬��2a��b��6��3��ֵ����____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶�ס����������ѧ��50�ˣ�Ϊ���˽���������ѧ��������������������˳�������������£��벹��������
�ռ����ݣ��Ӽס���������������ȡ10��ѧ�������������ʲ��Բ��Գɼ�(�ٷ���)���£�
�װࣺ65��75��75��80��60��50��75��90��85��65
�Ұࣺ90��55��80��70��55��70��95��80��65��70
��1�������������ݣ������·����������������������������ݣ�
�ɼ�x�����༶ | 50��x<60 | 60��x<70 | 70��x<80 | 80��x<90 | 90��x<100 |
�װ� | 1 | 3 | 3 | 2 | 1 |
�Ұ� | 2 | 1 | m | 2 | n |
�ڱ��У�m=________��n=________��
��2���������ݣ�
�������������ݵ�ƽ��������λ�������������ʾ��
�༶ | ƽ���� | ��λ�� | ���� |
�װ� | 75 | x | 75 |
�Ұ� | 72 | 70 | y |
�ڱ��У�x=________��y=________��
�����涨���Գɼ���80��(��80��)���ϵ�ѧ����������Ϊ����������Ұ�50��ѧ������������Ϊ�����ѧ����________�ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���![]() ��ͼ����
��ͼ����![]() ����
����![]() ����y���ڵ�C���������н��ۣ�
����y���ڵ�C���������н��ۣ�![]() ��b��
��b��![]() ��2��3��
��2��3��![]() ��
��![]() ����
����![]() ��
��![]() ��������ʵ��m��һ����
��������ʵ��m��һ����![]() ��
��![]() һԪ���η���
һԪ���η���![]() ������Ϊ
������Ϊ![]() ��
��![]() ��������ȷ�Ľ�����
��������ȷ�Ľ�����![]() ����
����![]()
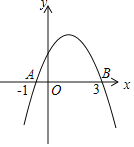
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij���̶��ڹ������û��ഹֱ������ǽAE��AF������������դ��Χ��һ�������γ���ABCD���м�������դ���ָ�����������Σ���դ���ܳ�180�ף���֪ǽAE��90�ף�ǽAF��Ϊ60�ף�
![]() ��
��![]() �ף���CDΪ______�ף��ı���ABCD�����Ϊ______��
�ף���CDΪ______�ף��ı���ABCD�����Ϊ______��![]() ��
��
![]() ��������ABCD�����Ϊ4000ƽ���ף���BCΪ�����ף�
��������ABCD�����Ϊ4000ƽ���ף���BCΪ�����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����⣺�䷽������ѧ��ѧ����Ҫ���������䷽���������С��ֵ������������ʵ��a��b���������±���a+b=![]() =
=![]() -2
-2![]() +2
+2![]() =
=![]() +2
+2![]() ���֡�
���֡�![]() ��0����
��0���� ![]() +2
+2![]() ��0+ 2
��0+ 2![]() ����a+b ��2
����a+b ��2![]() ��
��
��1�������������ݣ��ش��������⣺��a+b��2![]() ��a��b��Ϊ��ʵ�����У���abΪ��ֵp����a+b�� 2
��a��b��Ϊ��ʵ�����У���abΪ��ֵp����a+b�� 2![]() �����ҽ���a��b����________ʱ��a+b����Сֵ2
�����ҽ���a��b����________ʱ��a+b����Сֵ2![]() ��
��
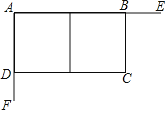
��2��˼����֤����ͼ1����ABC�У���ACB=90�㣬CD��AB������ΪD��COΪAB�������ߣ�AD��2a ��DB��2b, �Ը���ͼ����֤a+b��2![]() ��������ָ���Ⱥų���ʱ������.
��������ָ���Ⱥų���ʱ������.
��3��̽��Ӧ�ã���ͼ2����֪AΪ����������![]() ��ͼ����һ�㣬A��ĺ�����Ϊ1����һ�����ǰ��ֱ�Ƕ������A����ת��������ֱ�DZ�ʼ����x�ύ������D��E��F��0��-3��Ϊy����һ�㣬����DF��EF�����ı���ADFE�������Сֵ.
��ͼ����һ�㣬A��ĺ�����Ϊ1����һ�����ǰ��ֱ�Ƕ������A����ת��������ֱ�DZ�ʼ����x�ύ������D��E��F��0��-3��Ϊy����һ�㣬����DF��EF�����ı���ADFE�������Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ı�AB=20�����Ϊ320����BAD��90�㣬��O���AB��AD�����У�AO=10������O�İ뾶�����ڣ� ��

A��5 B��6 C��2![]() D��3
D��3![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com