
【题目】阅读理解:配方法是中学数学的重要方法,用配方法可求最大(小)值,对于任意正实数a、b,可作如下变形a+b=![]() =
=![]() -2
-2![]() +2
+2![]() =
=![]() +2
+2![]() ,又∵
,又∵![]() ≥0,∴
≥0,∴ ![]() +2
+2![]() ≥0+ 2
≥0+ 2![]() ,即a+b ≥2
,即a+b ≥2![]() .
.
(1)根据上述内容,回答下列问题:在a+b≥2![]() (a、b均为正实数)中,若ab为定值p,则a+b≥ 2
(a、b均为正实数)中,若ab为定值p,则a+b≥ 2![]() ,当且仅当a、b满足________时,a+b有最小值2
,当且仅当a、b满足________时,a+b有最小值2![]() .
.
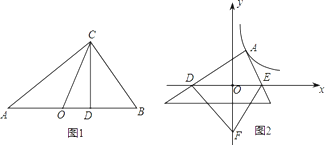
(2)思考验证:如图1,△ABC中,∠ACB=90°,CD⊥AB,垂足为D,CO为AB边上中线,AD=2a ,DB=2b, 试根据图形验证a+b≥2![]() 成立,并指出等号成立时的条件.
成立,并指出等号成立时的条件.
(3)探索应用:如图2,已知A为反比例函数![]() 的图象上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连接DF、EF,求四边形ADFE面积的最小值.
的图象上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连接DF、EF,求四边形ADFE面积的最小值.
【答案】(1)a=b ;(2)当D与O重合时或a=b时,等式成立;(3)28.
【解析】
(1)由给出的材料可知a=b时;
(2)因为AD=2a,DB=2b,所以AB=2a+2b,CO为中线,所以CO=a+b,再利用射影定理得CD=![]() ,在直角三角形COD中斜边大于直角边即CO>CD,问题得证;
,在直角三角形COD中斜边大于直角边即CO>CD,问题得证;
(3)把A点的横坐标为1,代入函数y=![]() 得,y=4,由(2)知:当DH=EH时,DE最小,此时S四边形ADFE=
得,y=4,由(2)知:当DH=EH时,DE最小,此时S四边形ADFE=![]() ×8×(4+3)=28.
×8×(4+3)=28.
(1)a=b,
(2)有已知得CO=a+b,CD=2![]() ,CO≥CD,即
,CO≥CD,即![]() ≥2
≥2![]() .
.
当D与O重合时或a=b时,等式成立.
(3)![]() ,
,

当DE最小时S四边形ADFE最小.
过A作AH⊥x轴,由(2)知:当DH=EH时,DE最小,
所以DE最小值为8,此时S四边形ADFE=![]() (4+3)=28.
(4+3)=28.


科目:初中数学 来源: 题型:
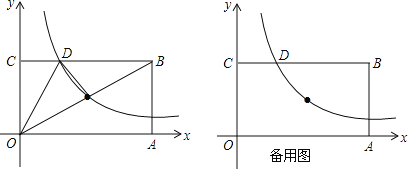
【题目】如图,已知矩形OABC的一个顶点B的坐标是(8,4),反比例函数y=![]() (x>0)的图象经过OB的中点E,且与边BC交于点D.
(x>0)的图象经过OB的中点E,且与边BC交于点D.
(1)求反比例函数的解析式和点D的坐标;
(2)求三角形DOE的面积;
(3)若过点D的直线y=mx+n将矩形OABC的面积分成3:5的两部分,求此直线解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校是乒乓球体育传统项目学校,为进一步推动该项目的开展,学校准备到体育用品店购买直拍球拍和横拍球拍若干副,并且每买一副球拍必须要买10个乒乓球,乒乓球的单价为2元/个,若购买20副直拍球拍和15副横拍球拍花费9000元;购买10副横拍球拍比购买5副直拍球拍多花费1600元.
(1)求两种球拍每副各多少元?
(2)若学校购买两种球拍共40副,且直拍球拍的数量不多于横拍球拍数量的3倍,请你给出一种费用最少的方案,并求出该方案所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 、
、![]() 、
、![]() 、
、![]() 各点的坐标分别为
各点的坐标分别为![]() 、
、![]() 、
、![]() 、
、![]() .
.

(1)在给出的图形中,画出四边形![]() 关于
关于![]() 轴对称的四边形
轴对称的四边形![]() ,并写出点
,并写出点![]() 和
和![]() 的坐标;
的坐标;
(2)在四边形![]() 内部画一条线段将四边形分割成两个等腰三角形,并直接写出两个等腰三角形的面积差.
内部画一条线段将四边形分割成两个等腰三角形,并直接写出两个等腰三角形的面积差.
查看答案和解析>>
科目:初中数学 来源: 题型:
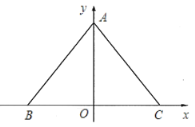
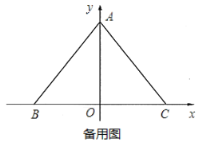
【题目】如图,![]() 在平面直角坐标系中,
在平面直角坐标系中,![]() ,
,![]() ,
,![]() ,点
,点![]() 、
、![]() 在
在![]() 轴上且关于
轴上且关于![]() 轴对称.
轴对称.

(1)求点![]() 的坐标;
的坐标;
(2)动点![]() 以每秒2个单位长度的速度从点
以每秒2个单位长度的速度从点![]() 出发沿
出发沿![]() 轴正方向向终点
轴正方向向终点![]() 运动,设运动时间为
运动,设运动时间为![]() 秒,点
秒,点![]() 到直线
到直线![]() 的距离
的距离![]() 的长为
的长为![]() ,求
,求![]() 与
与![]() 的关系式;
的关系式;
(3)在(2)的条件下,当点![]() 到
到![]() 的距离
的距离![]() 为
为![]() 时,连接
时,连接![]() ,作
,作![]() 的平分线分别交
的平分线分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
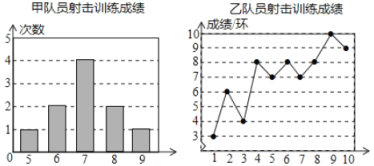
根据以上信息,整理分析数据如下:
平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
甲 |
|
|
|
|
乙 |
|
|
|
|
(1)![]() _ ;
_ ;![]() ;
;![]() ;
;
(2)填空:(填“甲”或“乙”),
①从平均数和中位数的角度来比较,成绩较好的是 ;
②从平均数和众数的角度来比较,成绩较好的是 ;
③成绩相对较稳定的是 ;
(3)若![]() 环以上有希望夺冠,选派其中一名参赛,你认为应选 队员.
环以上有希望夺冠,选派其中一名参赛,你认为应选 队员.
查看答案和解析>>
科目:初中数学 来源: 题型:
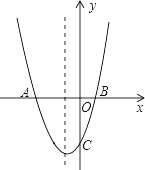
【题目】如图,已知:二次函数y=x2+bx+c 的图象与x轴交于A,B两点,其中A点坐标为(-3,0),与 y 轴交于点 C(0,-3)在抛物线上.
(1)求抛物线的表达式;
(2)抛物线的对称轴上有一动点 P,求出当 PB+PC 最小时点 P的坐标;
(3)若抛物线上有一动点Q,使△ABQ的面积为6,求Q点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是![]() 的中点,CE⊥AB于 E,BD交CE于点F.
的中点,CE⊥AB于 E,BD交CE于点F.
(1)若CD ﹦6, AC ﹦8,求⊙O的半径
(2)求证:CF﹦BF;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com