
【题目】如图,AB是⊙O的直径,C是![]() 的中点,CE⊥AB于 E,BD交CE于点F.
的中点,CE⊥AB于 E,BD交CE于点F.
(1)若CD ﹦6, AC ﹦8,求⊙O的半径
(2)求证:CF﹦BF;

【答案】(1)5;(2)证明见解析.
【解析】
(1)首先延长CE交⊙O于点P,由垂径定理可证得∠BCP=∠BDC,又由C是![]() 的中点,易证得∠BDC=∠CBD,继而可证得CF=BF;
的中点,易证得∠BDC=∠CBD,继而可证得CF=BF;
(2)由AB是⊙O的直径,根据直径所对的圆周角是直角,可得∠ACB=90°,然后由勾股定理求得AB的长,继而求得答案.
(1)∵AB是⊙O的直径,
∴∠ACB=90°,
∵CD=6,AC=8,
∴BC=6,
在Rt△ABC中,AB=![]() =10,
=10,
∴⊙O的半径为5.
(2)证明:延长CE交⊙O于点P,
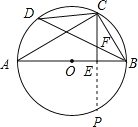
∵CE⊥AB,
∴![]() ,
,
∴∠BCP=∠BDC,
∵C是![]() 的中点,
的中点,
∴CD=CB,
∴∠BDC=∠CBD,
∴∠CBD=∠BCP,
∴CF=BF;


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】阅读理解:配方法是中学数学的重要方法,用配方法可求最大(小)值,对于任意正实数a、b,可作如下变形a+b=![]() =
=![]() -2
-2![]() +2
+2![]() =
=![]() +2
+2![]() ,又∵
,又∵![]() ≥0,∴
≥0,∴ ![]() +2
+2![]() ≥0+ 2
≥0+ 2![]() ,即a+b ≥2
,即a+b ≥2![]() .
.
(1)根据上述内容,回答下列问题:在a+b≥2![]() (a、b均为正实数)中,若ab为定值p,则a+b≥ 2
(a、b均为正实数)中,若ab为定值p,则a+b≥ 2![]() ,当且仅当a、b满足________时,a+b有最小值2
,当且仅当a、b满足________时,a+b有最小值2![]() .
.
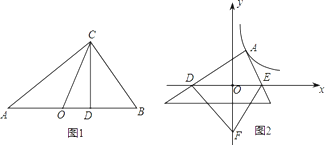
(2)思考验证:如图1,△ABC中,∠ACB=90°,CD⊥AB,垂足为D,CO为AB边上中线,AD=2a ,DB=2b, 试根据图形验证a+b≥2![]() 成立,并指出等号成立时的条件.
成立,并指出等号成立时的条件.
(3)探索应用:如图2,已知A为反比例函数![]() 的图象上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连接DF、EF,求四边形ADFE面积的最小值.
的图象上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连接DF、EF,求四边形ADFE面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于( )

A.5 B.6 C.2![]() D.3
D.3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图⊙O是ABC的外接圆,且AB=AC,点D在弧BC上运动,过点D作DE//BC,DE交AB的延长线于点E,连结AD、BD

(1)求证∠ADB=∠E;
(2)当点D运动到什么位置时,DE是⊙O的切线?请说明理由;
(3)当AB=5,BC=6时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:如图1:在四边形ABCD中,AB=AD,∠BAD=120 ,∠B=∠ADC=90°.E、F分别是 BC,CD 上的点。且∠EAF=60° . 探究图中线段BE,EF,FD 之间的数量关系。 小王同学探究此问题的方法是,延长 FD 到点 G,使 DG=BE,连结 AG,先证明△ABE≌△ADG, 再证明△AEF≌△AGF,可得出结论,他的结论应是_________;
探索延伸:如图2,若四边形ABCD中,AB=AD,∠B+∠D=180° .E,F 分别是 BC,CD 上的点,且∠EAF=![]() ∠BAD,上述结论是否仍然成立,并说明理由;
∠BAD,上述结论是否仍然成立,并说明理由;
实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东 70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以55 海里/小时的速度前进,舰艇乙沿北偏东 50°的方向以 75 海里/小时的速度前进2小时后, 指挥中心观测到甲、乙两舰艇分别到达 E,F 处,且两舰艇之间的夹角为70° ,试求此时两舰 艇之间的距离。

查看答案和解析>>
科目:初中数学 来源: 题型:
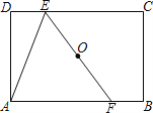
【题目】如图,在矩形ABCD中,AB=6,AD=4,过矩形ABCD的对角线交点O作直线分别交CD、AB于点E、F,连接AE,若△AEF是等腰三角形,则DE=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
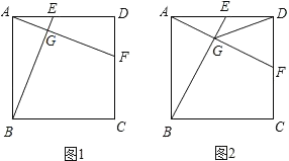
【题目】如图1,在正方形ABCD中,E,F分别是AD,CD上两点,BE交AF于点G,且DE=CF.
(1)写出BE与AF之间的关系,并证明你的结论;
(2)如图2,若AB=2,点E为AD的中点,连接GD,试证明GD是∠EGF的角平分线,并求出GD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com