
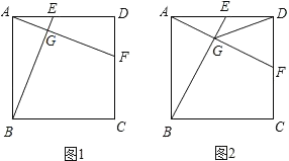
【题目】如图1,在正方形ABCD中,E,F分别是AD,CD上两点,BE交AF于点G,且DE=CF.
(1)写出BE与AF之间的关系,并证明你的结论;
(2)如图2,若AB=2,点E为AD的中点,连接GD,试证明GD是∠EGF的角平分线,并求出GD的长.
【答案】(1)BE=AF,BE⊥AF,理由见解析;(2)证明见解析,GD=![]() .
.
【解析】
(1)根据正方形的性质可证△BAE≌△ADF(SAS),得到BE=AF,∠ABE=∠DAF,进而得出∠BGA=90°即可;
(2)先利用勾股定理求出AF,进而利用面积求出DN,判断出AG=DN,在判断出DM=AG,即可得出GD是∠MGN的平分线,进而判断△DGN是等腰直角三角形即可得出结论.
解:(1)BE=AF,BE⊥AF,理由:
四边形ABCD是正方形,
∴BA=AD=CD,∠BAE=∠D=90°,
∵DE=CF,
∴AE=DE,
∴△BAE≌△ADF(SAS),
∴BE=AF,∠ABE=∠DAF,
∵∠ABE+∠AEB=90°,
∴∠DAE+∠AEB=90°,
∴∠BGA=90°,
∴BE⊥AF;
(2)如图2,过点D作DN⊥AF于N,DM⊥BE交BE的延长线于M,
在Rt△ADF中,根据勾股定理得,AF=![]() ,
,
∵S△ADF=![]() AD×FD=
AD×FD=![]() AD×DN,
AD×DN,
∴DN=![]() ,
,
∵△BAE≌△ADF,
∴S△BAE=S△ADF,
∵BE=AF,
∴AG=DN,
又∵∠AGE=∠DME,∠AEG=∠DEM
∴△AEG≌△DEM(AAS),
∴AG=DM,
∴DN=DM,
∵DM⊥BE,DN⊥AF,
∴GD平分∠MGN,
∴∠DGN=![]() ∠MGN=45°,
∠MGN=45°,
∴△DGN是等腰直角三角形,
∴GD=![]() DN=
DN=![]() .
.



科目:初中数学 来源: 题型:
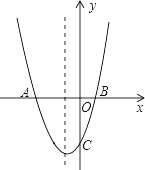
【题目】如图,已知:二次函数y=x2+bx+c 的图象与x轴交于A,B两点,其中A点坐标为(-3,0),与 y 轴交于点 C(0,-3)在抛物线上.
(1)求抛物线的表达式;
(2)抛物线的对称轴上有一动点 P,求出当 PB+PC 最小时点 P的坐标;
(3)若抛物线上有一动点Q,使△ABQ的面积为6,求Q点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是![]() 的中点,CE⊥AB于 E,BD交CE于点F.
的中点,CE⊥AB于 E,BD交CE于点F.
(1)若CD ﹦6, AC ﹦8,求⊙O的半径
(2)求证:CF﹦BF;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节前,安徽黄山脚下的小村庄的集市上,人山人海,还有人在摆“摸彩”游戏,只见他手拿一个黑色的袋子,内装大小、形状、质量完全相同的白球20只,且每一个球上都写有号码(1~20号)和1只红球,规定:每次只摸一只球.摸前交1元钱且在1~20内写一个号码,摸到红球奖5元,摸到号码数与你写的号码相同奖10元.
(1)你认为该游戏对“摸彩”者有利吗?说明你的理由.
(2)若一个“摸彩”者多次摸奖后,他平均每次将获利或损失多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=ax2+bx经过点A(2,4)和点B(6,0).
(1)求这条抛物线所对应的二次函数的解析式;
(2)直接写出它的开口方向、顶点坐标;
(3)点(x1,y1),(x2,y2)均在此抛物线上,若x1>x2>4,则y1 ________ y2(填“>”“=”或“<”).
查看答案和解析>>
科目:初中数学 来源: 题型:
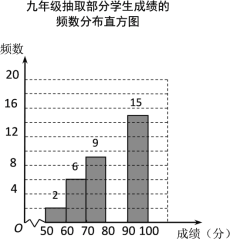
【题目】某校组织九年级学生参加汉字听写大赛,并随机抽取部分学生成绩作为样本进行分析,绘制成如下的统计表:
![]()
成绩x/分 | 频数 | 频率 | |
第1段 | x<60 | 2 | 0.04 |
第2段 | 60≤x<70 | 6 | 0.12 |
第3段 | 70≤x<80 | 9 | b |
第4段 | 80≤x<90 | a | 0.36 |
第5段 | 90≤x≤100 | 15 | 0.30 |
请根据所给信息,解答下列问题:
(1)a=______,b=______;
(2)请补全频数分布直方图;
(3)样本中,部分学生成绩的中位数落在第_______段;
(4)已知该年级有400名学生参加这次比赛,若成绩在90分以上(含90分)的为优,估计该年级成绩为优的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
(1)求k、b的值;
(2)若点D在y轴负半轴上,且满足S△COD=![]() S△BOC,求点D的坐标.
S△BOC,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=30°,点P在∠AOB的内部,P1与P关于OA对称,P2与P关于OB对称,则△P1OP2是
A. 含30°角的直角三角形 B. 顶角是30的等腰三角形
C. 等边三角形 D. 等腰直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一张三角形纸片![]() 如图甲
如图甲![]() ,其中
,其中![]() 将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为
将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为![]() 如图乙
如图乙![]() 再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为
再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为![]() 如图丙
如图丙![]() 原三角形纸片ABC中,
原三角形纸片ABC中,![]() 的大小为______
的大小为______![]()

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com