
【题目】如图,![]() 在平面直角坐标系中,
在平面直角坐标系中,![]() ,
,![]() ,
,![]() ,点
,点![]() 、
、![]() 在
在![]() 轴上且关于
轴上且关于![]() 轴对称.
轴对称.
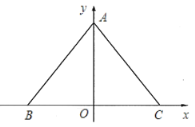
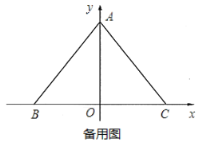

(1)求点![]() 的坐标;
的坐标;
(2)动点![]() 以每秒2个单位长度的速度从点
以每秒2个单位长度的速度从点![]() 出发沿
出发沿![]() 轴正方向向终点
轴正方向向终点![]() 运动,设运动时间为
运动,设运动时间为![]() 秒,点
秒,点![]() 到直线
到直线![]() 的距离
的距离![]() 的长为
的长为![]() ,求
,求![]() 与
与![]() 的关系式;
的关系式;
(3)在(2)的条件下,当点![]() 到
到![]() 的距离
的距离![]() 为
为![]() 时,连接
时,连接![]() ,作
,作![]() 的平分线分别交
的平分线分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,求
,求![]() 的长.
的长.
【答案】(1)C(4,0);(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据对称的性质知![]() 为等边三角形,利用直角三角形中30度角的性质即可求得答案;
为等边三角形,利用直角三角形中30度角的性质即可求得答案;
(2)利用面积法可求得![]() ,再利用坐标系中点的特征即可求得答案;
,再利用坐标系中点的特征即可求得答案;
(3)利用(2)的结论求得![]() ,利用角平分线的性质证得
,利用角平分线的性质证得![]() ,求得
,求得![]() ,利用面积法求得
,利用面积法求得![]() ,再利用直角三角形中30度角的性质即可求得答案.
,再利用直角三角形中30度角的性质即可求得答案.
(1)∵点![]() 、
、![]() 关于
关于![]() 轴对称,
轴对称,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 为等边三角形,
为等边三角形,
∴![]() ,
,
∴![]() ,
,
∴点C的坐标为:![]() ;
;
(2)连接![]() ,
,
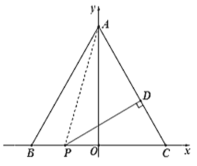
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
即:![]() ;
;
(3)∵点![]() 到
到![]() 的距离为
的距离为![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
延长![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,连接
,连接![]() 、
、![]() ,
,
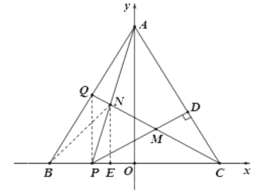
∵![]() 为
为![]() 的角平分线,
的角平分线,![]() 为等边三角形,
为等边三角形,
∴![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
设![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)如图所示,下列结论中:
①4ac-b2<0;②3b+2c<0;③4a+c<2b;④m(am+b)+b<a(m≠-1).
其中正确的结论有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级甲、乙两班各有学生50人,为了了解这两个班学生身体素质情况,进行了抽样调查过程如下,请补充完整,
收集数据:从甲、乙两个班各随机抽取10名学生进行身体素质测试测试成绩(百分制)如下:
甲班:65,75,75,80,60,50,75,90,85,65
乙班:90,55,80,70,55,70,95,80,65,70
(1)整理描述数据:按如下分数段整理、描述这两组样本数据:
成绩x人数班级 | 50≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x<100 |
甲班 | 1 | 3 | 3 | 2 | 1 |
乙班 | 2 | 1 | m | 2 | n |
在表中:m=________;n=________.
(2)分析数据:
①两组样本数据的平均数、中位数、众数如表所示:
班级 | 平均数 | 中位数 | 众数 |
甲班 | 75 | x | 75 |
乙班 | 72 | 70 | y |
在表中:x=________,y=________.
②若规定测试成绩在80分(含80分)以上的学生身体素质为优秀请估计乙班50名学生中身体素质为优秀的学生有________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
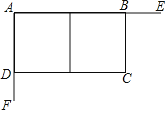
【题目】如图,某工程队在工地利用互相垂直的两面墙AE、AF,另两边用铁栅栏围成一个长方形场地ABCD,中间再用铁栅栏分割成两个长方形,铁栅栏总长180米,已知墙AE长90米,墙AF长为60米.
![]() 设
设![]() 米,则CD为______米,四边形ABCD的面积为______米
米,则CD为______米,四边形ABCD的面积为______米![]() ;
;
![]() 若长方形ABCD的面积为4000平方米,问BC为多少米?
若长方形ABCD的面积为4000平方米,问BC为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
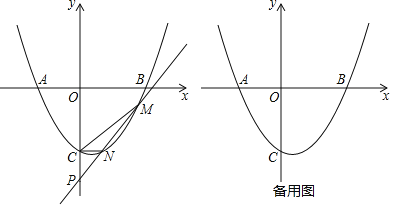
【题目】已知二次函数![]() 的图象对称轴为
的图象对称轴为![]() ,图象交x轴于A,B,交y轴于
,图象交x轴于A,B,交y轴于![]() ,且
,且![]() ,直线
,直线![]() 与二次函数图象交于M,
与二次函数图象交于M,![]() 在N的右边
在N的右边![]() ,交y轴于P.
,交y轴于P.
![]() 求二次函数图象的解析式;
求二次函数图象的解析式;
![]() 若
若![]() ,且
,且![]() 的面积为3,求k的值;
的面积为3,求k的值;
![]() 若
若![]() ,直线AN交y轴于Q,求
,直线AN交y轴于Q,求![]() 的值或取值范围.
的值或取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:配方法是中学数学的重要方法,用配方法可求最大(小)值,对于任意正实数a、b,可作如下变形a+b=![]() =
=![]() -2
-2![]() +2
+2![]() =
=![]() +2
+2![]() ,又∵
,又∵![]() ≥0,∴
≥0,∴ ![]() +2
+2![]() ≥0+ 2
≥0+ 2![]() ,即a+b ≥2
,即a+b ≥2![]() .
.
(1)根据上述内容,回答下列问题:在a+b≥2![]() (a、b均为正实数)中,若ab为定值p,则a+b≥ 2
(a、b均为正实数)中,若ab为定值p,则a+b≥ 2![]() ,当且仅当a、b满足________时,a+b有最小值2
,当且仅当a、b满足________时,a+b有最小值2![]() .
.
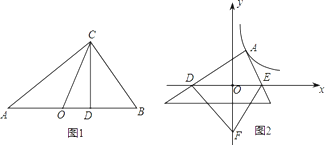
(2)思考验证:如图1,△ABC中,∠ACB=90°,CD⊥AB,垂足为D,CO为AB边上中线,AD=2a ,DB=2b, 试根据图形验证a+b≥2![]() 成立,并指出等号成立时的条件.
成立,并指出等号成立时的条件.
(3)探索应用:如图2,已知A为反比例函数![]() 的图象上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连接DF、EF,求四边形ADFE面积的最小值.
的图象上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连接DF、EF,求四边形ADFE面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
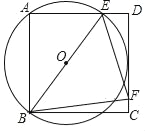
【题目】如图,正方形ABCD的边长为2,点E在边AD上(不与A,D重合),点F在边CD上,且∠EBF=45°,若△ABE的外接圆⊙O与CD边相切.
(1)求⊙O的半径长;
(2)求△BEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图⊙O是ABC的外接圆,且AB=AC,点D在弧BC上运动,过点D作DE//BC,DE交AB的延长线于点E,连结AD、BD

(1)求证∠ADB=∠E;
(2)当点D运动到什么位置时,DE是⊙O的切线?请说明理由;
(3)当AB=5,BC=6时,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com