
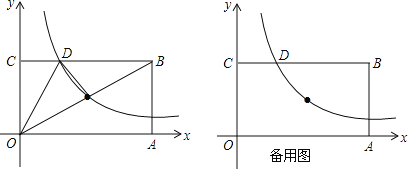
【题目】如图,已知矩形OABC的一个顶点B的坐标是(8,4),反比例函数y=![]() (x>0)的图象经过OB的中点E,且与边BC交于点D.
(x>0)的图象经过OB的中点E,且与边BC交于点D.
(1)求反比例函数的解析式和点D的坐标;
(2)求三角形DOE的面积;
(3)若过点D的直线y=mx+n将矩形OABC的面积分成3:5的两部分,求此直线解析式.
【答案】(1) 反比例函数解析式为y=![]() ,点D的坐标为(2,4);(2)三角形DOE的面积为6;
,点D的坐标为(2,4);(2)三角形DOE的面积为6;
(3) y=-2x+8或y=![]() x+
x+![]() .
.
【解析】
(1)根据中心对称求出点E的坐标, 再代入反比例函数解析式求出k, 然后根据点D的纵坐标与点B的纵坐标相等代入求解即可得到点D的坐标;
(2) 根据点D的坐标求出BD的长, 再由点E是OB的中点可知![]() ,由此可得出结论;
,由此可得出结论;
(3) 设直线与x轴的交点为F, 根据点D的坐标求出CD, 再根据梯形的面积分两种情况求出OF的长, 然后写出点F的坐标, 再利用待定系数法求一次函数的解析式即可.
解:(1)![]() 矩形OABC的顶点B的坐标是(8,4), E是矩形ABCD 的对称中心,
矩形OABC的顶点B的坐标是(8,4), E是矩形ABCD 的对称中心,
![]() 点E的坐标为(4,2),代入反比例函数解析式得
点E的坐标为(4,2),代入反比例函数解析式得![]() =2, 解得k=8,
=2, 解得k=8,
![]() 反比例函数解析式为y=
反比例函数解析式为y=![]()
![]() 点D在边BC上,
点D在边BC上,![]() 点D的纵坐标为4,
点D的纵坐标为4,
![]() y=4时, x=2,
y=4时, x=2,
![]() 点D的坐标为(2,4);
点D的坐标为(2,4);
(2)![]() D的坐标为(2,4),B(8,4),
D的坐标为(2,4),B(8,4),
![]() BD=6, OC=4.
BD=6, OC=4.
![]() 点E是OB的中点,
点E是OB的中点,
![]()
![]() =
=![]() =6
=6
(3) 如图, 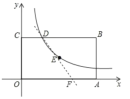
设直线与x轴的交点为F,矩形OABC的面积=8![]() 4=32,
4=32,
![]() 矩形OABC的面积分成3:5的两部分,
矩形OABC的面积分成3:5的两部分,
![]() 梯形OFDC的面积为
梯形OFDC的面积为![]() =12,或者
=12,或者![]() =20
=20
![]() 点D的坐标为(2,4),
点D的坐标为(2,4),
![]() 若
若![]() (2+OF)
(2+OF)![]() 4=12,
4=12,
解得OF=4,此时点F的坐标为(4,0),
若![]() (2+OF)
(2+OF)![]() 4=20,
4=20,
解得OF=8, 此时点F的坐标为(8,0),与A点重合,
当D(2,4),F(4,0)时,可得函数解析式为y=-2x+8
当D(2,4),F(8,0)时,可得函数解析式为y=![]() x+
x+![]()
综上所述,直线的解析式为y=-2x+8或y=![]() x+
x+![]() .
.


 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:
①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>﹣1时,y的值随x值的增大而增大;⑤当函数值y<0时,自变量x的取值范围是x<-1或x>5.
其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.
(1)在图1中以格点为顶点画一个面积为10的正方形;
(2)在图2中以格点为顶点画一个三角形,使三角形三边长分别为2、![]() 、
、![]() ;
;
(3)如图3,点A、B、C是小正方形的顶点,求∠ABC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育文化用品商店购进篮球和排球共200个,进价和售价如下表全部销售完后共获利润2600元.
类别 价格 | 篮球 | 排球 |
进价(元/个) | 80 | 50 |
售价(元/个) | 95 | 60 |
(1)求商店购进篮球和排球各多少个?
(2)王老师在元旦节这天到该体育文化用品商店为学校买篮球和排球各若干个(两种球都买了),商店在他的这笔交易中获利100元王老师有哪几种购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)如图所示,下列结论中:
①4ac-b2<0;②3b+2c<0;③4a+c<2b;④m(am+b)+b<a(m≠-1).
其中正确的结论有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,过B点作BM⊥AC于点E,交CD于点M,过D点作DN⊥AC于点F,交AB于点N.
(1)求证:四边形BMDN是平行四边形;
(2)已知AF=12,EM=5,求AN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知MB=ND,∠MBA=∠NDC,下列哪个条件不能判定△ABM≌△CDN( )

A.AM=CNB.AB=CD C.AM∥CN D.∠M=∠N
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:配方法是中学数学的重要方法,用配方法可求最大(小)值,对于任意正实数a、b,可作如下变形a+b=![]() =
=![]() -2
-2![]() +2
+2![]() =
=![]() +2
+2![]() ,又∵
,又∵![]() ≥0,∴
≥0,∴ ![]() +2
+2![]() ≥0+ 2
≥0+ 2![]() ,即a+b ≥2
,即a+b ≥2![]() .
.
(1)根据上述内容,回答下列问题:在a+b≥2![]() (a、b均为正实数)中,若ab为定值p,则a+b≥ 2
(a、b均为正实数)中,若ab为定值p,则a+b≥ 2![]() ,当且仅当a、b满足________时,a+b有最小值2
,当且仅当a、b满足________时,a+b有最小值2![]() .
.
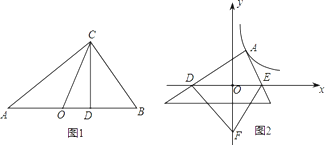
(2)思考验证:如图1,△ABC中,∠ACB=90°,CD⊥AB,垂足为D,CO为AB边上中线,AD=2a ,DB=2b, 试根据图形验证a+b≥2![]() 成立,并指出等号成立时的条件.
成立,并指出等号成立时的条件.
(3)探索应用:如图2,已知A为反比例函数![]() 的图象上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连接DF、EF,求四边形ADFE面积的最小值.
的图象上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连接DF、EF,求四边形ADFE面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com