
【题目】如图,二次函数![]() 的图象经过点
的图象经过点![]() ,点
,点![]() ,交y轴于点C,给出下列结论:
,交y轴于点C,给出下列结论:![]() :b:
:b:![]() :2:3;
:2:3;![]() 若
若![]() ,则
,则![]() ;
;![]() 对于任意实数m,一定有
对于任意实数m,一定有![]() ;
;![]() 一元二次方程
一元二次方程![]() 的两根为
的两根为![]() 和
和![]() ,其中正确的结论是
,其中正确的结论是![]()
![]()
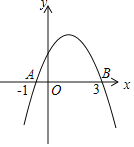
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
由抛物线上的两点坐标可以求出y=ax2+bx+c中a、b、c之间的倍数关系,可以用含有a的代数式表示b、c,再用带入求值法判定其它选项,具体见详解.
解:∵二次函数y=ax2+bx+c的图象经过点A(﹣1,0),点B(3,0),
∴抛物线解析式为y=a(x+1)(x﹣3),即y=ax2﹣2ax﹣3a,
∴b=﹣2a,c=﹣3a,
∴a:b:c=﹣1:2:3,故①正确;
当x=4时,y=a(x+1)(x﹣3)=a51=5a,y=ax2﹣2ax﹣3a=a[(x﹣1)2﹣4]=a(x﹣1)2﹣4a,
∴当0<x<4时,则5a<y<﹣4a,所以②错误;
∵y=ax2﹣2ax﹣3a=a[(x﹣1)2﹣4]=a(x﹣1)2﹣4a,
∴顶点坐标为(1,﹣4a),
∵抛物线开口向下, c=﹣3a,
∴抛物线向下平移﹣4a个单位,则抛物线顶点为(1,0),
∴平移后的解析式为:y′=ax2+bx+c+4a=ax2+bx﹣3a+4a=ax2+bx+a≤0,故③正确;
∵b=﹣2a,c=﹣3a,
∴方程cx2+bx+a=0化为﹣3ax2﹣2ax+a=0,
整理得3x2+2x﹣1=0,解得x1=﹣1,x2=![]() ,所以④正确.
,所以④正确.
故选:C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
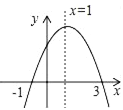
【题目】如图为二次函数y=ax2+bx+c的图象,给出下列说法:
①ab>0;
②方程ax2+bx+c=0的根为x1=﹣1,x2=3;
③a+b+c>0;
④当x>1时,随x值的增大而增大.
其中正确的说法有______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平面直角坐标系中,△ABC的三个顶点的坐标分别为A(2,2),B(1,﹣1),C(3,0).
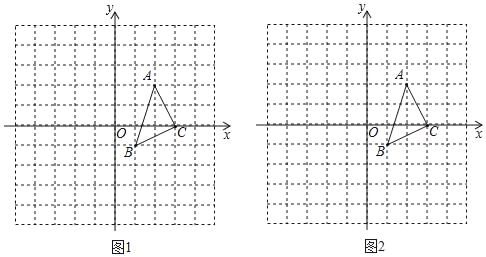
(1)在图1中,画出以点O为位似中心,放大△ABC到原来的2倍的△A1B1C1;
(2)若P(a,b)是AB边上一点,平移△ABC之后,点P的对应点P'的坐标是(a+3,b﹣2),在图2中画出平移后的△A2B2C2.
查看答案和解析>>
科目:初中数学 来源: 题型:
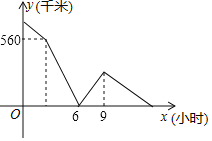
【题目】A、B、C三地在同一直线上,甲、乙两车分别从A,B两地相向匀速行驶,甲车先出发2小时,甲车到达B地后立即调头,并将速度提高10%后与乙车同向行驶,乙车到达A地后,继续保持原速向远离B的方向行驶,经过一段时间后两车同时到达C地,设两车之间的距离为y(千米),甲行驶的时间x(小时).y与x的关系如图所示,则B、C两地相距_____千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校是乒乓球体育传统项目学校,为进一步推动该项目的开展,学校准备到体育用品店购买直拍球拍和横拍球拍若干副,并且每买一副球拍必须要买10个乒乓球,乒乓球的单价为2元/个,若购买20副直拍球拍和15副横拍球拍花费9000元;购买10副横拍球拍比购买5副直拍球拍多花费1600元.
(1)求两种球拍每副各多少元?
(2)若学校购买两种球拍共40副,且直拍球拍的数量不多于横拍球拍数量的3倍,请你给出一种费用最少的方案,并求出该方案所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 、
、![]() 、
、![]() 、
、![]() 各点的坐标分别为
各点的坐标分别为![]() 、
、![]() 、
、![]() 、
、![]() .
.

(1)在给出的图形中,画出四边形![]() 关于
关于![]() 轴对称的四边形
轴对称的四边形![]() ,并写出点
,并写出点![]() 和
和![]() 的坐标;
的坐标;
(2)在四边形![]() 内部画一条线段将四边形分割成两个等腰三角形,并直接写出两个等腰三角形的面积差.
内部画一条线段将四边形分割成两个等腰三角形,并直接写出两个等腰三角形的面积差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
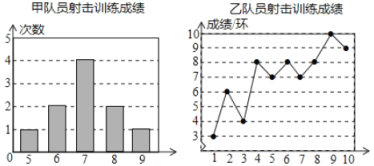
根据以上信息,整理分析数据如下:
平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
甲 |
|
|
|
|
乙 |
|
|
|
|
(1)![]() _ ;
_ ;![]() ;
;![]() ;
;
(2)填空:(填“甲”或“乙”),
①从平均数和中位数的角度来比较,成绩较好的是 ;
②从平均数和众数的角度来比较,成绩较好的是 ;
③成绩相对较稳定的是 ;
(3)若![]() 环以上有希望夺冠,选派其中一名参赛,你认为应选 队员.
环以上有希望夺冠,选派其中一名参赛,你认为应选 队员.
查看答案和解析>>
科目:初中数学 来源: 题型:
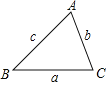
【题目】阅读材料:
如果一个三角形的三边长分别为a,b,c,记p=![]() ,那么这个三角形的面积S=
,那么这个三角形的面积S=![]() .这个公式叫“海伦公式”,它是利用三角形三条边的边长直接求三角形面积的公式。中国的秦九韶也得出了类似的公式,称三斜求积术,故这个公式又被称为“海伦秦---九韶公式”完成下列问题:
.这个公式叫“海伦公式”,它是利用三角形三条边的边长直接求三角形面积的公式。中国的秦九韶也得出了类似的公式,称三斜求积术,故这个公式又被称为“海伦秦---九韶公式”完成下列问题:
如图,在△ABC中,a=7,b=5,c=6.
(1)求△ABC的面积;
(2)设AB边上的高为h1,AC边上的高为h2,求h1 +h2的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com