
【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.
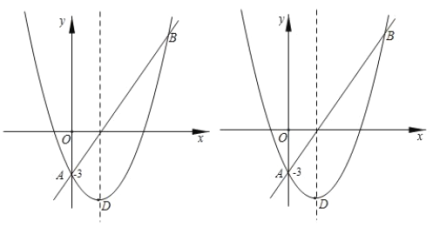
(1)求抛物线的解析式及顶点坐标;
(2)在![]() 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
【答案】(1)![]() ,顶点D(2,
,顶点D(2,![]() );(2)C(
);(2)C(![]() ,0)或(
,0)或(![]() ,0)或(
,0)或(![]() ,0);(3)
,0);(3)![]()
【解析】
(1)抛物线的顶点D的横坐标是2,则x![]() 2,抛物线过A(0,﹣3),则:函数的表达式为:y=ax2+bx﹣3,把B点坐标代入函数表达式,即可求解;
2,抛物线过A(0,﹣3),则:函数的表达式为:y=ax2+bx﹣3,把B点坐标代入函数表达式,即可求解;
(2)分AB=AC、AB=BC、AC=BC,三种情况求解即可;
(3)由S△PAB![]() PHxB,即可求解.
PHxB,即可求解.
(1)抛物线的顶点D的横坐标是2,则x![]() 2①,抛物线过A(0,﹣3),则:函数的表达式为:y=ax2+bx﹣3,把B点坐标代入上式得:9=25a+5b﹣3②,联立①、②解得:a
2①,抛物线过A(0,﹣3),则:函数的表达式为:y=ax2+bx﹣3,把B点坐标代入上式得:9=25a+5b﹣3②,联立①、②解得:a![]() ,b
,b![]() ,c=﹣3,∴抛物线的解析式为:y
,c=﹣3,∴抛物线的解析式为:y![]() x2
x2![]() x﹣3.
x﹣3.
当x=2时,y![]() ,即顶点D的坐标为(2,
,即顶点D的坐标为(2,![]() );
);
(2)A(0,﹣3),B(5,9),则AB=13,设点C坐标(m,0),分三种情况讨论:
①当AB=AC时,则:(m)2+(﹣3)2=132,解得:m=±4![]() ,即点C坐标为:(4
,即点C坐标为:(4![]() ,0)或(﹣4
,0)或(﹣4![]() ,0);
,0);
②当AB=BC时,则:(5﹣m)2+92=132,解得:m=5![]() ,即:点C坐标为(5
,即:点C坐标为(5![]() ,0)或(5﹣2
,0)或(5﹣2![]() ,0);
,0);
③当AC=BC时,则:5﹣m)2+92=(m)2+(﹣3)2,解得:m=![]() ,则点C坐标为(
,则点C坐标为(![]() ,0).
,0).
综上所述:存在,点C的坐标为:(±4![]() ,0)或(5
,0)或(5![]() ,0)或(
,0)或(![]() ,0);
,0);
(3)过点P作y轴的平行线交AB于点H.设直线AB的表达式为y=kx﹣3,把点B坐标代入上式,9=5k﹣3,则k![]() ,故函数的表达式为:y
,故函数的表达式为:y![]() x﹣3,设点P坐标为(m,
x﹣3,设点P坐标为(m,![]() m2
m2![]() m﹣3),则点H坐标为(m,
m﹣3),则点H坐标为(m,![]() m﹣3),S△PAB
m﹣3),S△PAB![]() PHxB
PHxB![]() (
(![]() m2+12m)=-6m2+30m=
m2+12m)=-6m2+30m=![]() ,当m=
,当m=![]() 时,S△PAB取得最大值为:
时,S△PAB取得最大值为:![]() .
.
答:△PAB的面积最大值为![]() .
.


科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,以BC为直径的半圆O与边AB相交于点D,切线DE⊥AC,垂足为点E.
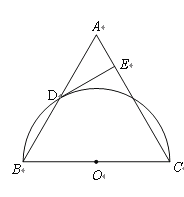
求证:(1)△ABC是等边三角形;
(2)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系 xOy 中,已知正比例函数 y1=﹣2x 的图象与反比例函数 y2=![]() 的图象交于 A(﹣1,a),B 两点.
的图象交于 A(﹣1,a),B 两点.
(1)求出反比例函数的解析式及点 B 的坐标;
(2)观察图象,请直接写出满足 y≤2 的取值范围;
(3)点 P 是第四象限内反比例函数的图象上一点,若△POB 的面积为 1,请直接写出点 P的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
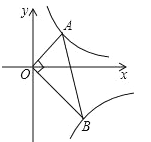
【题目】已知点A、B分别在反比例函数![]() (x>0),
(x>0),![]() (x>0)的图象上,且∠AOB=90°,则∠B=30°,则k的取值为( )
(x>0)的图象上,且∠AOB=90°,则∠B=30°,则k的取值为( )
A. ![]() B.
B. ![]() C. ﹣2 D. ﹣3
C. ﹣2 D. ﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为4的正六边形ABCDEF的中心与坐标原点O重合,AF∥x轴,将该正六边形绕原点O顺时针旋转n次,每次旋转60°,当n=63时,顶点F的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校数学兴趣小组在探究如何求tan15°的值,经过自主思考、合作交流讨论,得到以下思路:
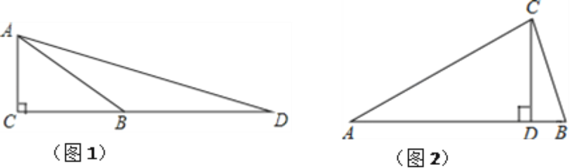
思路一 如图1,在Rt△ABC中,∠C=90°,∠ABC=30°,延长CB至点D,使BD=BA,连接AD.……
思路二 如图2,在顶角为30°的等腰三角形ABC中,AB=AC,若过点C作CD⊥AB于点D,则∠BCD=15°……
思路三 利用科普书上的有关公式:tan(α+β)=![]() ;
;
tan(α―β)=![]() ;…
;…
请解决下列问题(上述思路仅供参考).
(1)选择你喜欢的一种思路,完成解答过程,求出tan 15°的值(保留根号);
(2)试利用同样的方法,计算tan22.5°的值(保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形 ABCD 中,点 E,F 分别在 BC 和 AB 上,BE=3,AF=2,BF=4,将△ BEF 绕点 E 顺时针旋转,得到△GEH,当点 H 落在 CD 边上时,F,H 两点之间的距离为_____.
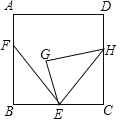
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系y=mx2+20x+n,其图象如图所示.
(1)m=_____,n=_____.
(2)销售单价为多少元时,该种商品每天的销售利润最大?最大利润为多少元?
(3)该种商品每天的销售利润不低于16元时,直接写出x的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com