
【题目】已知点A、B分别在反比例函数![]() (x>0),
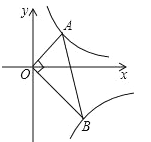
(x>0),![]() (x>0)的图象上,且∠AOB=90°,则∠B=30°,则k的取值为( )
(x>0)的图象上,且∠AOB=90°,则∠B=30°,则k的取值为( )
A. ![]() B.
B. ![]() C. ﹣2 D. ﹣3
C. ﹣2 D. ﹣3
【答案】D
【解析】
过A作AC垂直于y轴,过B作BD垂直于y轴,易证△AOC∽△OBD,利用反比例函数k的几何意义求出两三角形的面积,得出面积比,在直角三角形AOB中,利用锐角三角函数定义即可求出tan∠B的值,即OA与OB的比值,利用面积比等于相似比的平方,即可求出k值.
过A作AC⊥y轴,过B作BD⊥y轴,可得:∠ACO=∠BDO=90°,∴∠AOC+∠OAC=90°.
∵OA⊥OB,∴∠AOC+∠BOD=90°,∴∠OAC=∠BOD.
∵∠ACO=∠ODB=90°,∴△AOC∽△OBD.
∵点A、B分别在反比例函数y![]() (x>0),y
(x>0),y![]() (x>0)的图象上,∴S△AOC
(x>0)的图象上,∴S△AOC![]() ,S△OBD=|
,S△OBD=|![]() |,∴S△AOC:S△OBD=1:|k|,∴(
|,∴S△AOC:S△OBD=1:|k|,∴(![]() )2=1:|k|.在Rt△AOB中,tanB
)2=1:|k|.在Rt△AOB中,tanB![]() ,∴1:|k|=1:3,∴|k|=3.
,∴1:|k|=1:3,∴|k|=3.
∵y![]() (x>0)的图象在第四象限,∴k=﹣3.
(x>0)的图象在第四象限,∴k=﹣3.
故选D.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:
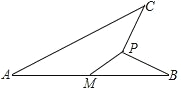
【题目】如图,线段 AB=4,M 为 AB 的中点,动点 P 到点 M 的距离是 1,连接 PB,线段
PB 绕点 P 逆时针旋转 90°得到线段 PC,连接 AC,则线段 AC 长度的最大值是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx+b的图象是直线l,点A(![]() ,
,![]() )在反比例函数y=
)在反比例函数y=![]() 的图象上.
的图象上.
(1)求m的值;
(2)如图,若直线l与反比例函数的图象相交于M、N两点,不等式kx+b>![]() 的解集为1<x<2,求一次函数的表达式;
的解集为1<x<2,求一次函数的表达式;
(3)当b=4时,一次函数与反比例函数的图象有两个交点,求k的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“爱我永州”中学生演讲比赛中,五位评委分别给甲、乙两位选手的评分如下:
甲:8、8、9、8、7乙:7、9、9、6、9
则下列说法中错误的是( )
A.甲、乙得分的平均数都是8
B.甲得分的众数是8,乙得分的众数是9
C.甲得分的中位数是9,乙得分的中位数是6
D.甲得分的方差比乙得分的方差小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣5,1),B(﹣2,2),C(﹣1,4),请按下列要求画图:
(1)将△ABC先向右平移4个单位长度、再向下平移1个单位长度,得到△A1B1C1,画出△A1B1C1;
(2)画出与△ABC关于原点O成中心对称的△A2B2C2,并直接写出点A2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.
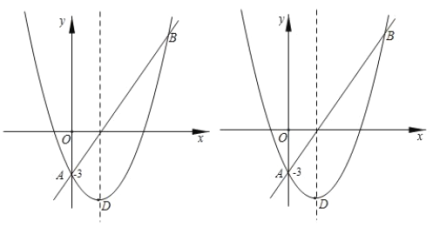
(1)求抛物线的解析式及顶点坐标;
(2)在![]() 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,∠BAD=90°,过C作CE⊥AD垂足为E,且∠EDC=∠BDC.
(1)求证:CE是⊙O的切线;
(2)若DE+CE=4,AB=6,求BD的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校是乒乓球体育传统项目学校,为进一步推动该项目的开展,学校准备到体育用品店购买直拍球拍和横拍球拍若干副,并且每买一副球拍必须要买10个乒乓球,乒乓球的单价为2元/个,若购买20副直拍球拍和15副横拍球拍花费9000元;购买10副横拍球拍比购买5副直拍球拍多花费1600元.
(1)求两种球拍每副各多少元?
(2)若学校购买两种球拍共40副,且直拍球拍的数量不多于横拍球拍数量的3倍,请你给出一种费用最少的方案,并求出该方案所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 某次学生夏令营活动,有小学生、初中生、高中生和大学生参加,共200人,各类学生人数比例见扇形统计图.
(1)参加这次夏令营活动的初中生共有______人.
(2)活动组织者号召参加这次夏令营活动的所有学生为贫困学生捐款.结果小学生每人捐款5元,初中生每人捐款10元,高中生每人捐款15元,大学生每人捐款20元,平均每人捐款多少元?
(3)在(2)的条件下,把每个学生的捐款数(以元为单位)一一记录下来,则在这组数据中,众数和中位数分别是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com