
【题目】在“爱我永州”中学生演讲比赛中,五位评委分别给甲、乙两位选手的评分如下:
甲:8、8、9、8、7乙:7、9、9、6、9
则下列说法中错误的是( )
A.甲、乙得分的平均数都是8
B.甲得分的众数是8,乙得分的众数是9
C.甲得分的中位数是9,乙得分的中位数是6
D.甲得分的方差比乙得分的方差小
【答案】C
【解析】
分别求出甲、乙的平均数、众数、中位数及方差可逐一判断.
解:A、甲得分的平均数为(8+8+9+8+7)÷5=8,乙得分的平均数为(7+9+9+6+9)÷5=8,故选项不符合;
B、甲得分次数最多是8分,即众数为8,乙得分最多的是9分,即众数为9,故此选项不符合;
C、∵甲得分从小到大排列为:7、8、8、8、9,∴甲的中位数是8分;∵乙得分从小到大排列为:6、7、9、9、9,∴乙的中位数是9分;故此选项符合;
D、S甲2=![]() ×[(8-8)2+(7-8)2+(9-8)2+(8-8)2+(8-8)2]=
×[(8-8)2+(7-8)2+(9-8)2+(8-8)2+(8-8)2]=![]() ×2=0.4,
×2=0.4,
S乙2=![]() ×[(7-8)2+(9-8)2+(6-8)2+(9-8)2+(9-8)2]=
×[(7-8)2+(9-8)2+(6-8)2+(9-8)2+(9-8)2]=![]() ×8=1.6,
×8=1.6,
S甲2<S乙2,故此选项不符合.
故选C.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
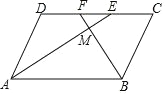
【题目】如图,在 ABCD 中,AE、BF 分别平分∠DAB 和∠ABC,交 CD 于点 E、F,AE、BF 相交于点 M.
(1)求证:AE⊥BF;
(2)判断线段 DF 与 CE 的大小关系,并予以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
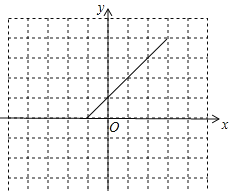
【题目】我们知道,把直线y=x向左平移1个单位可得到一次函数y=x+1的图象,把直线y=kx(k≠0)向左平移1个单位可得到一次函数y=k(x+1)的图象,把抛物线y=ax2(a≠0)向左平移1个单位,可得到二次函数y=a(x+1)2的图象.类似的:我们将函数y=∣x∣向左平移1个单位,在平面直角坐标系中画出了新函数的部分图象,并请回答下列问题:
(1)平移后的函数解析式是__________;
(2)借助下列表格,用你认为最简单的方法补画平移后的函数图象:
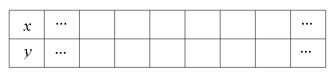
(3)当x 时,y随x的增大而增大;当x 时,y随x的增大而减小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系 xOy 中,已知正比例函数 y1=﹣2x 的图象与反比例函数 y2=![]() 的图象交于 A(﹣1,a),B 两点.
的图象交于 A(﹣1,a),B 两点.
(1)求出反比例函数的解析式及点 B 的坐标;
(2)观察图象,请直接写出满足 y≤2 的取值范围;
(3)点 P 是第四象限内反比例函数的图象上一点,若△POB 的面积为 1,请直接写出点 P的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四部不同的电影,分别记为A、B、C、D.
(1)若甲从中随机选择一部观看,则恰好是电影A的概率是 ;
(2)若甲从中随机选择一部观看,乙也从中随机选择一部观看,用列表或画树状图的方法列出所有等可能的结果,并求甲、乙两人恰好选择同一部电影的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
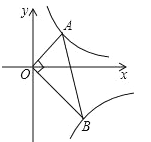
【题目】已知点A、B分别在反比例函数![]() (x>0),
(x>0),![]() (x>0)的图象上,且∠AOB=90°,则∠B=30°,则k的取值为( )
(x>0)的图象上,且∠AOB=90°,则∠B=30°,则k的取值为( )
A. ![]() B.
B. ![]() C. ﹣2 D. ﹣3
C. ﹣2 D. ﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校数学兴趣小组在探究如何求tan15°的值,经过自主思考、合作交流讨论,得到以下思路:
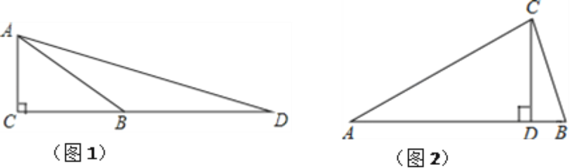
思路一 如图1,在Rt△ABC中,∠C=90°,∠ABC=30°,延长CB至点D,使BD=BA,连接AD.……
思路二 如图2,在顶角为30°的等腰三角形ABC中,AB=AC,若过点C作CD⊥AB于点D,则∠BCD=15°……
思路三 利用科普书上的有关公式:tan(α+β)=![]() ;
;
tan(α―β)=![]() ;…
;…
请解决下列问题(上述思路仅供参考).
(1)选择你喜欢的一种思路,完成解答过程,求出tan 15°的值(保留根号);
(2)试利用同样的方法,计算tan22.5°的值(保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
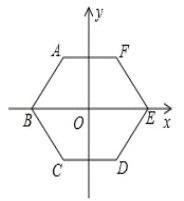
【题目】如图,边长为6的正六边形ABCDEF的中心与坐标原点O重合,AF∥x轴.将正六边形绕原点逆时针旋转n次,每次旋转60°,当n=2019时,顶点A的坐标为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com