
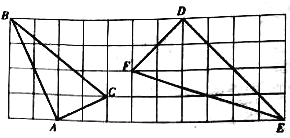
【题目】如图,在由边长均为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点(网格线的交点)上,请按要求完成下列各题.
(1)试证明△ABC是直角三角形;
(2)判断△ABC和△DEF是否相似,并说明理由.
 名师点拨卷系列答案
名师点拨卷系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=![]() ,O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE,CF.
,O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE,CF.
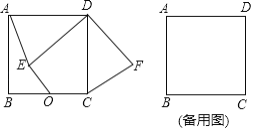
(1)求证:AE=CF;
(2)若A,E,O三点共线,连接OF,求线段OF的长.
(3)求线段OF长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
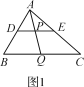
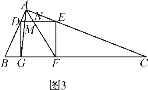
【题目】类比、转化、从特殊到一般等思想方法在数学学习和研究中经常用到,如下是一个案例,请补充完整.
原题:如图1,在△ABC中,点D,E,Q分别在AB,AC,BC上,且DE∥BC,AQ交DE于点P,求证:![]() =
=![]() .
.
(1)尝试探究:在图1中,由DP∥BQ,得△ADP___△ABQ(填“≌”或“∽”),则![]() =___,同理可得
=___,同理可得![]() =
=![]() ,从而
,从而![]() =
=![]() ;
;
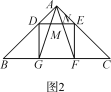
(2)类比延伸:如图2,在△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG,AF分别交DE于M,N两点,若AB=AC=1,则MN的长为_____;
(3)拓展迁移:如图3,在△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG,AF分别交DE于M,N两点,AB<AC,求证:MN2=DM·EN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将正方形网格放置在平面直角坐标系中,其中每个小正方形的边长均为1,△ABC经过平移后得到△A1B1C1,若AC上一点P(1.2,1.4)平移后对应点为P1,点P1绕原点顺时针旋转180°,对应点为P2,则点P2的坐标为( )

A. (2.8,3.6) B. (﹣2.8,﹣3.6)
C. (3.8,2.6) D. (﹣3.8,﹣2.6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠BAC的平分线与线段BC的垂直平分线PQ相交于点P,过点P分别作PN垂直于AB于点N,PM垂直于AC于点M,BN和CM有什么数量关系?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
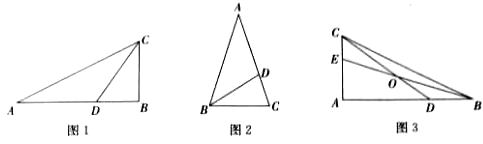
【题目】我们知道,若线段上的个点把这条线段分制为两部分,其中较长的一部分与全长之比等于![]() 时,则这个点称为黄金分割点。类比三角形中线的定义,我们规定:连接三角形的一个顶点和它对边的黄金分割点的线段叫做该三角形的黄金分割线.
时,则这个点称为黄金分割点。类比三角形中线的定义,我们规定:连接三角形的一个顶点和它对边的黄金分割点的线段叫做该三角形的黄金分割线.
(1)如图1,CD是△ABC的黄金分割线(AD> BD),△ABC的面积为4,求△ACD的面积 ;
(2)如图2,在△ABC中,∠A= 36°,AB=AC=1,过点B作BD平分∠ABC,与AC相交于点D,求证: BD是△ABC的黄金分割线.
(3)如图3,BE、CD是△ABC的黄金分割线(AD> BD,AE> CE),BE、CD相交于点O.
①设△BOD与△COE的面积分别为S1、S2 ,请猜想S1、S2之间的数量关系,并说明理由;
②求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
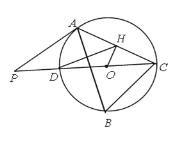
【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若OH⊥AC,OH=1,求DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
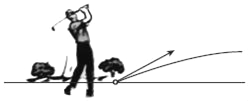
【题目】如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系h=20t﹣5t2.
(1)求小球飞行3s时的高度;
(2)问:小球的飞行高度能否达到22m?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
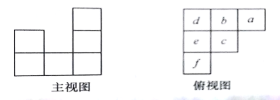
【题目】用小立方体搭一个几何体,使它的主视图和俯视图如图所示,俯视图中小正方形中字母表示在该位置小立方体的个数,请解答下列问题:
(1)求![]() 的值;
的值;
(2)这个几何体最少有几个小立方体搭成,最多有几个小立方体搭成;
(3)当![]() 时画出这个几何体的左视图.
时画出这个几何体的左视图.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com