
 如图,在四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°.
如图,在四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°.分析 (1)连接AC,先根据勾股定理求得AC的长,再根据勾股定理的逆定理,求得∠D=90°即可;
(2)根据△ACD和△ACB的面积之和等于四边形ABCD的面积,进行计算即可.
解答 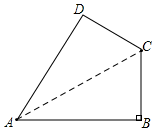 解:连接AC.
解:连接AC.
∵AB=20,BC=15,∠B=90°,
∴由勾股定理,得AC2=202+152=625.
又∵CD=7,AD=24,
∴CD2十AD2=625,
∴AC2=CD2+AD2,
∴∠D=90°;
(2)四边形ABCD的面积=△ACD的面积+△ACB的面积
=$\frac{1}{2}$×BC×AB+$\frac{1}{2}$×DC×AD
=$\frac{1}{2}$×15×20+$\frac{1}{2}$×7×24
=234.
点评 本题主要考查了勾股定理以及勾股定理的逆定理的综合运用,解决问题时需要区别勾股定理及其逆定理.通过作辅助线,将四边形问题转化为三角形问题是关键.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案科目:初中数学 来源: 题型:解答题
 如图,某轮船在海上以每小时30海里的速度向正西方向航行,上午8:00在点B处测得小岛A在北偏东30°方向,上午9:00船到达C处,测得岛A在北偏东45°方向,如果轮船继续向西航行,上午11:00到达点D处,求点D与小岛A的距离(精确到0.1海里)
如图,某轮船在海上以每小时30海里的速度向正西方向航行,上午8:00在点B处测得小岛A在北偏东30°方向,上午9:00船到达C处,测得岛A在北偏东45°方向,如果轮船继续向西航行,上午11:00到达点D处,求点D与小岛A的距离(精确到0.1海里)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
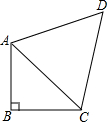 如图,∠ABC=90°,$\frac{AB}{AC}$=$\frac{\sqrt{7}}{4}$,BC=6,AD=DC,∠ADC=60°.
如图,∠ABC=90°,$\frac{AB}{AC}$=$\frac{\sqrt{7}}{4}$,BC=6,AD=DC,∠ADC=60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
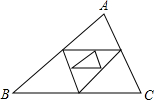 如图,△ABC周长为1,连接△ABC三边中点构成第二个三角形,再连接第二个三角形三边中点构成第三个三角形,以此类推,第2016个三角形的周长为( )
如图,△ABC周长为1,连接△ABC三边中点构成第二个三角形,再连接第二个三角形三边中点构成第三个三角形,以此类推,第2016个三角形的周长为( )| A. | 22016 | B. | 22017 | C. | ${(\frac{1}{2})}^{2016}$ | D. | ${(\frac{1}{2})}^{2015}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
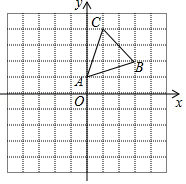 如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.
如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
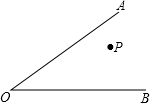 如图,点P为∠AOB内一定点,小明从点P出发,先到达OA边上的某一位置M,再达到OB边上的某一位置N,最后返回点P.设计一条路线,使小明走的总路径最短,在图中确定此时点M和点N的位置(保留画图痕迹,但不写画法).
如图,点P为∠AOB内一定点,小明从点P出发,先到达OA边上的某一位置M,再达到OB边上的某一位置N,最后返回点P.设计一条路线,使小明走的总路径最短,在图中确定此时点M和点N的位置(保留画图痕迹,但不写画法).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com