
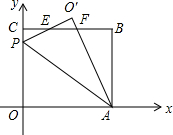
 在平面直角坐标系中,O是坐标原点,矩OABC的位置如图所示,点A,C的坐标分别为(10,0),(0,8),点P是y轴上的一个动点,将△OAP沿AP翻折得到:△O′AP,直线BC与直线O′P交于点E,与直线O′A交于点F.
在平面直角坐标系中,O是坐标原点,矩OABC的位置如图所示,点A,C的坐标分别为(10,0),(0,8),点P是y轴上的一个动点,将△OAP沿AP翻折得到:△O′AP,直线BC与直线O′P交于点E,与直线O′A交于点F.分析 (1)先在RT△ABO′求出BO′,设PO=PO′=x,在RT△PCO′中利用勾股定理解决即可.
(2)当∠CPE=∠APO时得∠CPE=∠APO=∠APO′=60°求出OP=$\frac{\sqrt{3}}{3}$OA即可.当∠CPE=∠OAP时,∠CEP=∠APO=∠APO′,此时AP∥EC,显然不可能.
(3)分四种情形讨论,在RT△PCE中利用E2=PC2+CE2,列出方程即可.
解答 解:(1)图1,当O′落在直线BC上时,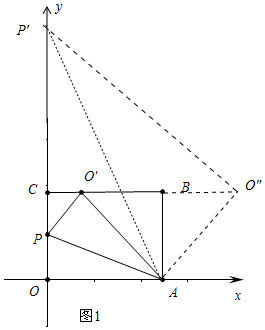
在RT△ABO′中,∵AO′=10,AB=8,
∴BO′=$\sqrt{AO{′}^{2}-A{B}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
∵△APO′是由△AOP翻折,
∴可以设PO=PO′=x,
在RT△PCO′中,∵PO′2=PC2+CO′2,
∴x2=(8-x)2+42,
∴x=5,
∴AP=$\sqrt{O{P}^{2}+A{O}^{2}}$=$\sqrt{{5}^{2}+1{0}^{2}}$=5$\sqrt{5}$,
当O″在CB的延长线上时,设CP′=y,
则有y2+162=(y+8)2,
∴y=12,
∴OP′=20,
AP′=$\sqrt{1{0}^{2}+2{0}^{2}}$=10$\sqrt{5}$,
综上所述,当O′落在直线BC上时,求折痕AP的长为5$\sqrt{5}$或10$\sqrt{5}$.
(2)当∠CPE=∠APO时,
∵∠CPE=∠APO=∠APO′=60°,
∴OP=$\frac{\sqrt{3}}{3}$OA=$\frac{10\sqrt{3}}{3}$,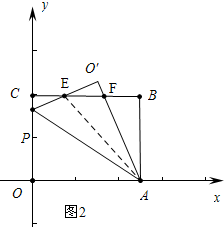
设直线AP为y=kx+b,由题意$\left\{\begin{array}{l}{b=\frac{10\sqrt{3}}{3}}\\{10k+b=0}\end{array}\right.$解得$\left\{\begin{array}{l}{k=-\frac{\sqrt{3}}{3}}\\{b=\frac{10\sqrt{3}}{3}}\end{array}\right.$,
∴直线AP为y=-$\frac{\sqrt{3}}{3}$x+$\frac{10\sqrt{3}}{3}$.
当∠CPE=∠OAP时,∠CEP=∠APO=∠APO′,此时AP∥EC,显然不可能.
(3)情形1如图2中,∵CE=$\frac{1}{5}$BC=2,
∴BE=8,AE=$\sqrt{E{B}^{2}+A{B}^{2}}$=8$\sqrt{2}$,EO′=$\sqrt{A{E}^{2}-AO{′}^{2}}$=2$\sqrt{7}$,
设OP=x,在RT△PCE中,∵PE2=PC2+CE2,
∴(x-2$\sqrt{7}$)2=(8-x)2+22,
∴x=$\frac{10(4+\sqrt{7})}{9}$,此时P[0,$\frac{10(4+\sqrt{7})}{9}$],
情形2如图3中,同理O′E=2$\sqrt{7}$,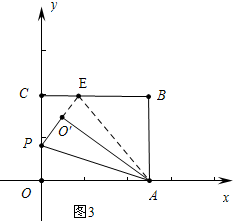
设OP=x,在RT△PCE中,∵PE2=PC2+CE2,
∴(x+2$\sqrt{7}$)2=(8-x)2+22,
∴x=$\frac{10(4-\sqrt{7})}{9}$,此时P[0,$\frac{10(4-\sqrt{7})}{9}$],
情形3如图4中,AE=$\sqrt{E{B}^{2}+A{B}^{2}}$=$\sqrt{1{2}^{2}+{8}^{2}}$=4$\sqrt{13}$,
EO′=$\sqrt{A{E}^{2}-AO{′}^{2}}$=6$\sqrt{3}$,
设OP=x,在RT△PCE中,∵PE2=PC2+CE2,
∴(6$\sqrt{3}$-x)2=(x-8)2+22,
∴x=$\frac{10(3\sqrt{3}+4)}{11}$,此时P[0,$\frac{10(3\sqrt{3}+4)}{11}$],
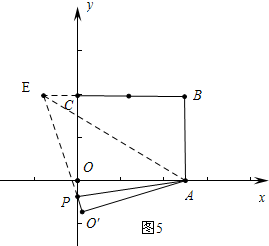
情形4如图5中,设OP=x,在RT△PCE中,∵PE2=PC2+CE2,
∴(6$\sqrt{3}$-x)2=(x+8)2+22,
∴x=$\frac{10(3\sqrt{3}-4)}{11}$,此时P[0,$\frac{10(3\sqrt{3}-4)}{11}$].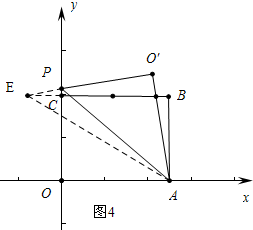
点评 本题考查矩形的性质、勾股定理等知识,用到转化的思想,分类讨论的方法,灵活运用勾股定理是解题的关键,分类讨论时考虑问题要全面.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
 如图,已知∠ADE=60°,DF平分∠ADE,∠1=30°,试说明:DF∥BE.
如图,已知∠ADE=60°,DF平分∠ADE,∠1=30°,试说明:DF∥BE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠C=90°,AC=3cm,BC=4cm,P、Q分别为AB、BC上的动点,点P从点A出发沿AB方向作匀速移动的同时,点Q从点B出发沿BC方向向点C作匀速移动,移动的速度均为1cm/s,设P、Q移动的时间为t(0<t≤4).
如图,在△ABC中,∠C=90°,AC=3cm,BC=4cm,P、Q分别为AB、BC上的动点,点P从点A出发沿AB方向作匀速移动的同时,点Q从点B出发沿BC方向向点C作匀速移动,移动的速度均为1cm/s,设P、Q移动的时间为t(0<t≤4).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 当n<0时,m<0 | B. | 当n>0时,m>x2 | C. | 当n<0时,x1<m<x2 | D. | 当n>0时,x2>m>x1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,弦CD⊥AB于点H,⊙O的切线EF与AC平行,且与CD的延长线交于点E,与AB的延长线交于点F,切点为G,连接AG交CD于K.
如图,AB是⊙O的直径,弦CD⊥AB于点H,⊙O的切线EF与AC平行,且与CD的延长线交于点E,与AB的延长线交于点F,切点为G,连接AG交CD于K.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com