Question

（1）如图1，△ABC和△ADE均为顶角为α的等腰三角形，连接BD、CE，BD与CE、AC分别交于点O、点P．通过观察或测量，猜想：
①线段BD和CE的数量关系为______．
②BD和CE之间的夹角∠BOC=______．
（2）现将图1中的△ADE绕着点A顺时针旋转一个角度，得到图2，BD的延长线与CE的延长线交于点O，与AC交于点P，问（1）中猜想的结论还成立吗？若成立，予以证明；若不成立，说明理由．

Answer 1

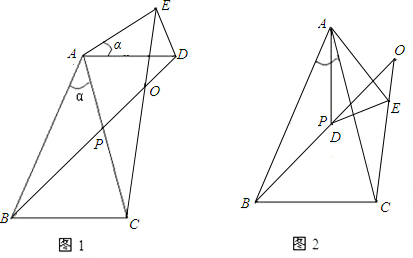
解：（1）①相等；②α．
证明：∵△ABC和△ADE均为顶角为α的等腰三角形，
∴∠BAD=α+∠CAD，∠CAE=α+∠CAD，AB=AC，AD=AE，
∴∠BAD=∠CAE，
∴△BAD≌△CAE（SAS），
∴BD=CE，∠ABD=∠ACE，
∵∠ABC+∠ACB=∠ABD+∠OBC+∠ACB=∠ACE+∠OBC+∠ACB=∠OBC+∠OCB=180°-α，
∴∠BOC=180°-（∠OBC+∠OCB）=α；

（2）成立．
证明：∵△ABC和△ADE均为顶角为α的等腰三角形，
∴∠BAD=α-∠CAD，∠CAE=α-∠CAD，AB=AC，AD=AE，
∴∠BAD=∠CAE，
∴△BAD≌△CAE（SAS），
∴BD=CE，∠ABD=∠ACE，
∵∠ABC+∠ACB=∠ABD+∠OBC+∠ACB=∠ACE+∠OBC+∠ACB=∠OBC+∠OCB=180°-α，
∴∠BOC=180°-（∠OBC+∠OCB）=α．
分析：（1）由△ABC和△ADE均为顶角为α的等腰三角形，易证得∠BAD=∠CAE，又由AB=AC，AD=AE，根据SAS即可证得△BAD≌△CAE，即可证得BD=CE，∠ABD=∠ACE，继而可证得∠BOC=α；
（2）方法同（1），首先利用SAS证得△BAD≌△CAE，由全等三角形的性质，即可证得结论正确．
点评：此题考查了等腰三角形的性质，全等三角形的判定与性质，以及旋转的性质．此题综合性较强，难度适中，解题的关键是注意数形结合思想的应用．