
【题目】已知,如图AB∥CD,∠B=80°,∠BCE=20°,∠CEF=80°,请判断AB与EF的位置关系,并说明理由.

解:理由如下:
∵AB∥CD
∴∠B=∠BCD .
∵∠B=80°,
∴∠BCD=80° .
∵∠BCE=20°,
∴∠ECD=100°,
又∵∠CEF=80°
∴ + =180°,
∴EF∥
又∵AB∥CD,
∴AB∥EF .
【答案】AB∥EF,理由见解析;填空答案:AB∥EF,两直线平行,内错角相等;等量代换,∠E,∠DCE,CD,同旁内角互补,两直线平行;平行于同一直线的两条直线互相平行.
【解析】
根据平行线的性质,可得∠BCD=80°,进而可得到∠E+∠ECD=180°,可证明EF∥CD,由平行的“传递性”可证明结论.
AB∥EF,理由如下:
∵AB∥CD,
∴∠B=∠BCD,(两直线平行,内错角相等)
∵∠B=80°,
∴∠BCD=80°,(等量代换)
∵∠BCE=20°,
∴∠ECD=100°,
∵∠CEF=80°,
∴∠E+∠DCE=180°,
∴EF∥CD,(同旁内角互补,两直线平行)
∴AB∥EF.(平行于同一条直线的两条直线互相平行)


科目:初中数学 来源: 题型:
【题目】如图,把△ABC先向上平移3个单位长度,再向右平移2个单位长度,得到△A1B1C1.

(1)在图中画出△A1B1C1,并写出点A1、B1、C1的坐标;
(2)连接A1A、C1C,则四边形A1ACC1的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中:①PA=PB;②△AOP≌△BOP;③OA=OB;④PO平分∠APB.其中成立的有________(填写正确的序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
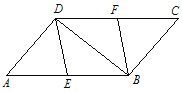
【题目】如图,在□ABCD 中,∠ADB=90°,点 E 为 AB 边的中点,点 F 为CD 边的中点.
(1)求证:四边形 DEBF 是菱形;
(2)当∠A 等于多少度时,四边形 DEBF 是正方形?并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0)…根据这个规律探究可得,第100个点的坐标为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一边是另一边的![]() 倍的三角形叫做智慧三角形,这两边中较长边称为智慧边,这两边的 夹角叫做智慧角.
倍的三角形叫做智慧三角形,这两边中较长边称为智慧边,这两边的 夹角叫做智慧角.
(1)在 Rt△ABC 中,∠ACB=90°,若∠A 为智慧角,则∠B 的度数为 ;
(2)如图①,在△ABC 中,∠A=45°,∠B=30°,求证:△ABC 是智慧三角形;
(3)如图②,△ABC 是智慧三角形,BC 为智慧边,∠B 为智慧角,A(3,0),点 B,C 在函数 y=![]() (x>0)的图像上,点 C 在点 B 的上方,且点 B 的纵坐标为
(x>0)的图像上,点 C 在点 B 的上方,且点 B 的纵坐标为![]() .当△ABC是直角三角形时,求 k 的值.
.当△ABC是直角三角形时,求 k 的值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60,请你探究OE,EF之间有什么数量关系?并证明你的结论。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平面直角坐标系中,抛物线y=ax2+bx+3与x轴的两个交点分别为A(﹣3,0),B(1,0),与y轴的交点为D,对称轴与抛物线交于点C,与x轴负半轴交于点H.

(1)求抛物线的表达式;
(2)点E,F分别是抛物线对称轴CH上的两个动点(点E在点F上方),且EF=1,求使四边形BDEF的周长最小时的点E,F坐标及最小值;
(3)如图2,点P为对称轴左侧,x轴上方的抛物线上的点,PQ⊥AC于点Q,是否存在这样的点P使△PCQ与△ACH相似?若存在请求出点P的坐标,若不存在请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com