
【题目】如图1,边形![]() 为菱形,点
为菱形,点![]() 为对角线
为对角线![]() 上的一个动点,连接
上的一个动点,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)如图1,求证:![]() ;
;
(2)如图2,若![]() ,且
,且![]() ,求
,求![]() 的度数.
的度数.


【答案】(1)见解析;(2)60°
【解析】
(1)根据菱形的性质得出∠BCE=∠DCE,BC=CD,AB∥CD,推出∠AFD=∠CDE,证△BCE≌△DCE,推出∠CBE=∠CDE即可.(2)由(1)可知,∠EDC=∠EBC,通过DE=EC从而得出∠ DCA=30°,从而得出答案
证明:
(1)∵四边形ABCD是菱形,
∴∠BCE=∠DCE,BC=CD,AB∥CD,
∴∠AFD=∠CDE,
∵BC=CD,∠BCE=∠DCE,CE=CE
∴△BCE≌△DCE,
∴∠CBE=∠CDE,
∵∠AFD=∠CDE,
∴∠AFD=∠CBE.
(2)∵DE=CE;
∴∠ EDC=∠ ECD
由(1)知∠EDC=∠ EBC,∠ CAD=∠ CAB,
设∠EDC=∠ ECD=∠ CBE=x;
∵AB∥CD,
∴∠DCB=∠CBF=2x,
∵BE⊥AF,
∴∠EBF=∠EBC+∠CBF=x+2x=3x=90°,则x=30°;
∴∠DAB=60°.


科目:初中数学 来源: 题型:
【题目】为引导学生“爱读书,多读书,读好书”,某校七(2)班决定购买A、B两种书籍.若购买A种书籍1本和B种书籍3本,共需要180元;若购买A种书籍3本和B种书籍1本,共需要140元.
(1)求A、B两种书籍每本各需多少元?
(2)该班根据实际情况,要求购买A、B两种书籍总费用不超过700元,并且购买B种书籍的数量是A种书籍的![]() ,求该班本次购买A、B两种书籍有哪几种方案?
,求该班本次购买A、B两种书籍有哪几种方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与y轴正半轴相交,其顶点坐标为(
的图象与y轴正半轴相交,其顶点坐标为(![]() ,1),下列结论:①abc>0;②a=b;③a=4c﹣4;④方程
,1),下列结论:①abc>0;②a=b;③a=4c﹣4;④方程![]() 有两个相等的实数根,其中正确的结论是______.(只填序号即可).
有两个相等的实数根,其中正确的结论是______.(只填序号即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上 A,B,C 三个点对应的数分别为 a,b,x,且 A,B 到-2 所对应的点的距离都等于 6,点 B在点 A 的右侧.
(1)请在数轴上表示点 A,B 位置,a= ,b= ;
(2)请用含 x 的代数式表示 CB= ;
(3)若点 C 在点 B 的左侧,且 CB=8,点 A 以每秒 2 个单位长度的速度沿数轴向右运动,当 AC=2AB时,求点 A 移动的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图AB∥CD,∠B=80°,∠BCE=20°,∠CEF=80°,请判断AB与EF的位置关系,并说明理由.

解:理由如下:
∵AB∥CD
∴∠B=∠BCD .
∵∠B=80°,
∴∠BCD=80° .
∵∠BCE=20°,
∴∠ECD=100°,
又∵∠CEF=80°
∴ + =180°,
∴EF∥
又∵AB∥CD,
∴AB∥EF .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【题目】如图①,一次函数 y=![]() x - 2 的图像交 x 轴于点 A,交 y 轴于点 B,二次函数 y=
x - 2 的图像交 x 轴于点 A,交 y 轴于点 B,二次函数 y=![]() x2 bx c的图像经过 A、B 两点,与 x 轴交于另一点 C.
x2 bx c的图像经过 A、B 两点,与 x 轴交于另一点 C.
(1)求二次函数的关系式及点 C 的坐标;
(2)如图②,若点 P 是直线 AB 上方的抛物线上一点,过点 P 作 PD∥x 轴交 AB 于点 D,PE∥y 轴交 AB 于点 E,求 PD+PE 的最大值;
(3)如图③,若点 M 在抛物线的对称轴上,且∠AMB=∠ACB,求出所有满足条件的点 M的坐标.
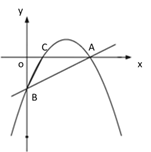
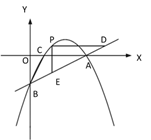
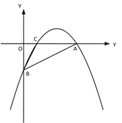
① ② ③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以直线AB上一点O为端点作射线OC,使∠BOC=70°,将一个直角三角板的直角顶点放在点O处(∠DOE=90°).
(1)如图①,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图②,将直角三角板DOE绕点O转动,若OD恰好平分∠BOC,求∠AOE的度数。
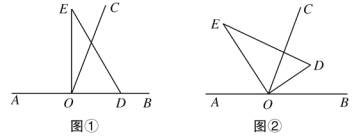
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)探索材料1(填空):
数轴上表示数![]() 和数
和数![]() 的两点之间的距离等于
的两点之间的距离等于![]() .例如数轴上表示数2和5的两点距离为
.例如数轴上表示数2和5的两点距离为![]() ;数轴上表示数3和-1的两点距离为
;数轴上表示数3和-1的两点距离为![]() ;则
;则![]() 的意义可理解为数轴上表示数 和 这两点的距离;
的意义可理解为数轴上表示数 和 这两点的距离;![]() 的意义可理解为数轴上表示数 和 这两点的距离;
的意义可理解为数轴上表示数 和 这两点的距离;
(2)探索材料2(填空):
①如图1,在工厂的一条流水线上有两个加工点![]() 和
和![]() ,要在流水线上设一个材料供应点
,要在流水线上设一个材料供应点![]() 往两个加工点输送材料,材料供应点
往两个加工点输送材料,材料供应点![]() 应设在 才能使
应设在 才能使![]() 到
到![]() 的距离与
的距离与![]() 到
到![]() 的距离之和最小?
的距离之和最小?

②如图2,在工厂的一条流水线上有三个加工点![]() 要在流水线上设一个材料供应点
要在流水线上设一个材料供应点![]() 往三个加工点输送材料,材料供应点
往三个加工点输送材料,材料供应点![]() 应设在 才能使
应设在 才能使![]() 到
到![]() 三点的距离之和最小?
三点的距离之和最小?

③如图3,在工厂的一条流水线上有四个加工点![]() ,要在流水线上设一个材料供应点
,要在流水线上设一个材料供应点![]() 往四个加工点输送材料,材料供应点
往四个加工点输送材料,材料供应点![]() 应设在 才能使
应设在 才能使![]() 到
到![]() 四点的距离之和最小?
四点的距离之和最小?

(3)结论应用(填空):
①代数式![]() 的最小值是 ,此时
的最小值是 ,此时![]() 的范围是 ;
的范围是 ;
②代数式![]() 的最小值是 ,此时
的最小值是 ,此时![]() 的值为 .
的值为 .
③代数式![]() 的最小值是 ,此时
的最小值是 ,此时![]() 的范围是 .
的范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小淇在说明 “直角三角形斜边上的中线等于斜边的一半”是真命题,部分思路如下:如图,在∠ACB内做∠BCD=∠B,CD与AB相交于点D,…….请根据以上思路,完成证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com