
分析 由方程x2+px+q=0有2个相同的实数根,得到△1=p2-4q=0,而对于方程x2-p(1+q)x+q3+2q2+q=0的判别式△2=[p(1+q)]2-4(q3+2q2+q)=p2(1+q)2-4q(1+q)2=(p2-4q)(1+q)2,故△2=0,结论得证.
解答 解:∵方程x2+px+q=0有2个相同的实数根,
∴△1=p2-4q=0,
而对于方程x2-p(1+q)x+q3+2q2+q=0,
其判别式△2=[p(1+q)]2-4(q3+2q2+q)
=p2(1+q)2-4q(1+q)2
=(p2-4q)(1+q)2=0,
∴方程x2-p(1+q)x+q3+2q2+q=0有2个相同的实数根.
点评 本题主要考查了一元二次方程根的判别式:△=b2-4ac,当△>0时方程有两个不等实根,△=0时方程有两个相等实根,△<0时方程没有实根.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
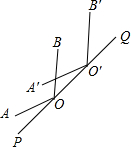 如图,点O在直线PQ上,∠AOP=20°,将∠AOB沿PQ方向平移一段距离后得到∠A′O′B′,且有∠B′O′Q=40°,则∠AOB的度数为( )
如图,点O在直线PQ上,∠AOP=20°,将∠AOB沿PQ方向平移一段距离后得到∠A′O′B′,且有∠B′O′Q=40°,则∠AOB的度数为( )| A. | 120° | B. | 140° | C. | 150° | D. | 160° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com