
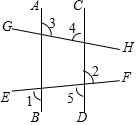
 请你帮小明把下面的证明过程补充完整.
请你帮小明把下面的证明过程补充完整. 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 16℃ | B. | -16℃ | C. | 20℃ | D. | -20℃ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
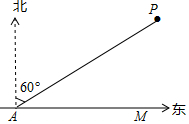 如图,在一计划修建的东西走向的铁路AM旁有一自然保护区P,在距该自然保护区中心P的15$\sqrt{2}$ km圆形区域内属于保护区范围,线路勘察队在距保护区中心P的30km的A处测得保护区中心P位于A的北偏东60°方向,若不改变铁路的原修建线路,铁路是否会破坏该保护区的保护区域?请通过计算加以说明.如果会破坏,铁路自A处开始至少沿东偏南多少度改线,才不会破坏该保护区的保护区域?
如图,在一计划修建的东西走向的铁路AM旁有一自然保护区P,在距该自然保护区中心P的15$\sqrt{2}$ km圆形区域内属于保护区范围,线路勘察队在距保护区中心P的30km的A处测得保护区中心P位于A的北偏东60°方向,若不改变铁路的原修建线路,铁路是否会破坏该保护区的保护区域?请通过计算加以说明.如果会破坏,铁路自A处开始至少沿东偏南多少度改线,才不会破坏该保护区的保护区域?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
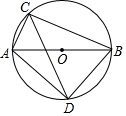 如图,AB是⊙O的直径,弦BC长为$4\sqrt{2}$,弦AC长为2,∠ACB的平分线交⊙O于点D.
如图,AB是⊙O的直径,弦BC长为$4\sqrt{2}$,弦AC长为2,∠ACB的平分线交⊙O于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
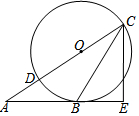 如图,已知△ABC的边AB是⊙O的切线,切点为B,AC经过圆心O并与圆相交于点D、C.过C作直线CE⊥AB,交AB的延长线于点E.
如图,已知△ABC的边AB是⊙O的切线,切点为B,AC经过圆心O并与圆相交于点D、C.过C作直线CE⊥AB,交AB的延长线于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com