
分析 (1)根据幂的乘方、负整数指数幂和零指数幂可以解答本题;
(2)根据积的乘方、同底数幂的乘法和除法可以解答本题;
(3)根据平方差公式可以解答本题;
(4)根据提公因式法可以解答本题.
解答 解:(1)(-1)2016+(-$\frac{1}{2}$)-2-(3.14-π)0
=1+4-1
=4;
(2)(2x3y)2•(-2x3y)+(-2x3y)3÷(2x2)
=4x6y2•(-2x3y)+(-8x9y3)÷(2x2)
=-8x9y3-4x7y3;
(3)1232-122×124
=1232-(123-1)×(123+1)
=1232-1232+1
=1;
(4)(2x-3)2-(2x+3)(2x-3)
=(2x-3)[(2x-3)-(2x+3)]
=(2x-3)×(-6)
=-12x+18.
点评 本题考查整式的混合运算、零指数幂、负整数指数幂,解题的关键是明确它们各自的计算方法.


科目:初中数学 来源: 题型:解答题
 如图,在直角坐标系中,已知点A的坐标为(6,0),点B(x,y)在第一象限内,且满足x+y=8,设△AOB的面积是S.
如图,在直角坐标系中,已知点A的坐标为(6,0),点B(x,y)在第一象限内,且满足x+y=8,设△AOB的面积是S.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
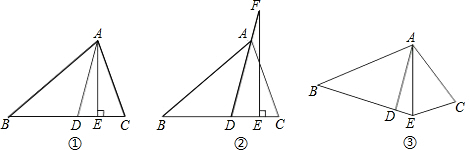
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
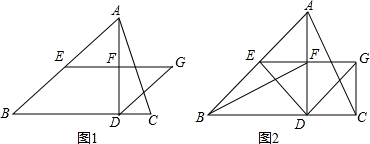
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com