
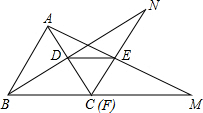
 等边三角形ABC和等边三角形DEF,D在AC边上.延长BD交CE延长线于N,延长AE交BC延长线于M.
等边三角形ABC和等边三角形DEF,D在AC边上.延长BD交CE延长线于N,延长AE交BC延长线于M. 证明:∵△ABC和△DEF为等边三角形,
证明:∵△ABC和△DEF为等边三角形,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
| ||
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
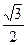 AB,
AB,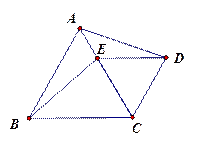
查看答案和解析>>
科目:初中数学 来源:2011届江苏省常州市武进区星辰实验学校初三第一学期期中数学卷doc 题型:解答题
(10分)
如图,等边三角形ABC和等边三角形DEC,CE和AC重合,CE= AB,
AB,
(1)求证:AD=BE;
(2)若CE绕点C顺时针旋转30度,连BD交AC于点G,取AB的中点F连FG,求证:BE=2FG;
(3)在(2)的条件下AB=2,则AG= ______.(直接写出结果)
查看答案和解析>>
科目:初中数学 来源:2012届浙江省义乌市初中毕业生学业模拟考试数学试卷(带解析) 题型:解答题
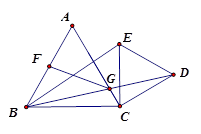
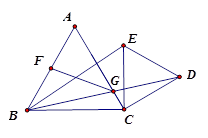
如图,等边三角形ABC和等边三角形DEC,CE和AC重合,CE=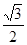 AB,
AB,
(1)求证:AD=BE;
(2)若CE绕点C顺时针旋转30度,连BD交AC于点G,取AB的中点F连FG,求证:BE=2FG;
(3)在(2)的条件下AB=2,则AG= ______.(直接写出结果)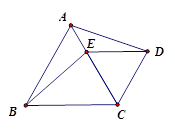
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com