
分析 (1)把点(2,1)代入反比例函数y=$\frac{k}{x}$即可得出k,再把k的值和点(2,1)代入一次函数y=kx+b即可得出一次函数的解析式;
(2)根据关于x轴对称点的坐标,得出点P′坐标,再代入判断是否在一次函数y=kx+b的图象上.
解答 解:(1)把点(2,1)代入反比例函数y=$\frac{k}{x}$,
得k=2,
∴反比例函数解析式为$y=\frac{2}{x}$,
把点(2,1)和k=2代入y=kx+b,得4+b=1,
∴b=-3,
∴一次函数解析式为y=2x-3;
(2)∵点P(-1,-5)关于x轴的对称点P′,
∴P′(-1,5),
当x=-1,y=-2-3=-5,
∴P′(-1,5)不在函数一次函数y=2x-3的图象上.
点评 本题考查了反比例函数和一次函数的交点问题,掌握用待定系数法求反比例函数和一次函数的解析式即可.


科目:初中数学 来源: 题型:填空题
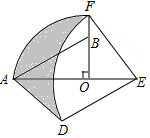 如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是8-π.
如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是8-π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
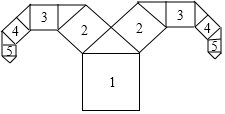 如图所示是一种“牛头形”图案,其作法是:从正方形1开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形2,依此类推下去,若正方形1的边长为16cm,则正方形6的边长为( )
如图所示是一种“牛头形”图案,其作法是:从正方形1开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形2,依此类推下去,若正方形1的边长为16cm,则正方形6的边长为( )| A. | 1cm | B. | 2$\sqrt{2}$cm | C. | 3cm | D. | 4cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
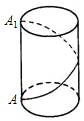 如图,一只蚂蚁沿着图示的路线从圆柱高AA1的端点A到达A1,若圆柱底面半径为$\frac{6}{π}$,高为5,蚂蚁爬行的最短距离为多少?
如图,一只蚂蚁沿着图示的路线从圆柱高AA1的端点A到达A1,若圆柱底面半径为$\frac{6}{π}$,高为5,蚂蚁爬行的最短距离为多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com