
分析 (1)根据平方差公式可以解答本题;
(2)根据题目中的式子,进行变形建立与所求式子之间的关系,注意所求的式子的结果是正值.
解答 解:(1)∵$\sqrt{39+{x}^{2}}$-$\sqrt{15+{x}^{2}}$=2,
∴($\sqrt{39+{x}^{2}}$-$\sqrt{15+{x}^{2}}$)($\sqrt{39+{x}^{2}}$+$\sqrt{15+{x}^{2}}$)=2($\sqrt{39+{x}^{2}}$+$\sqrt{15+{x}^{2}}$),
∴39+x2-15-x2=2($\sqrt{39+{x}^{2}}$+$\sqrt{15+{x}^{2}}$),
∴24=2($\sqrt{39+{x}^{2}}$+$\sqrt{15+{x}^{2}}$),
∴$\sqrt{39+{x}^{2}}$+$\sqrt{15+{x}^{2}}$=12;
(2)∵$\sqrt{29-{x}^{2}}$-$\sqrt{15+{x}^{2}}$=2,
∴($\sqrt{29-{x}^{2}}$-$\sqrt{15+{x}^{2}}$)2=4,
∴$29-{x}^{2}+15+{x}^{2}-2\sqrt{29-{x}^{2}}•\sqrt{15+{x}^{2}}=4$,
∴$\sqrt{29-{x}^{2}}•\sqrt{15+{x}^{2}}=20$,
∴($\sqrt{29-{x}^{2}}$+$\sqrt{15+{x}^{2}}$)2=$29-{x}^{2}+15+{x}^{2}+2\sqrt{29-{x}^{2}}•\sqrt{15+{x}^{2}}$=44+2×20=84,
∴$\sqrt{29-{x}^{2}}$+$\sqrt{15+{x}^{2}}$=$\sqrt{84}=2\sqrt{21}$.
点评 本题考查二次根式的化简求值,解答此类问题的关键是明确二次根式化简求值的方法.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
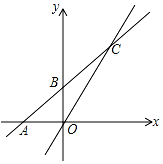 已知一次函数y=kx+b 的图象与x轴交于点A,与y轴交于点B(0,2),且与正比例函数y=$\frac{4}{3}$x的图象交于点C(m,4)
已知一次函数y=kx+b 的图象与x轴交于点A,与y轴交于点B(0,2),且与正比例函数y=$\frac{4}{3}$x的图象交于点C(m,4)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
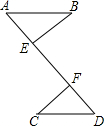 如图,已知BE⊥AD,CF⊥AD,垂足分别为E、F,则在下列各组条件中选择一组,其中不能判定Rt△ABE≌Rt△DCF的是( )
如图,已知BE⊥AD,CF⊥AD,垂足分别为E、F,则在下列各组条件中选择一组,其中不能判定Rt△ABE≌Rt△DCF的是( )| A. | AB=DC,∠B=∠C | B. | AB=DC,AB∥CD | C. | AB=DC,BE=CF | D. | AB=DF,BE=CF |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com