
| A. | $5\sqrt{5}-5$ | B. | $5\sqrt{5}+1$ | C. | 10$\sqrt{5}$-20 | D. | $15-5\sqrt{5}$ |
分析 根据黄金比是$\frac{\sqrt{5}-1}{2}$进行计算即可.
解答 解: ∵P是线段AB的黄金分割点,
∵P是线段AB的黄金分割点,
∴AQ=$\frac{\sqrt{5}-1}{2}$AB=5$\sqrt{5}$-5,
Q是线段AB的两个黄金分割点,
∴BP=$\frac{\sqrt{5}-1}{2}$AB=5$\sqrt{5}$-5,
∴PQ=AQ+BP-AB=10$\sqrt{5}$-20,
故选:C.
点评 本题考查的是黄金分割的概念,掌握把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值$\frac{\sqrt{5}-1}{2}$叫做黄金比是解题的关键.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:解答题
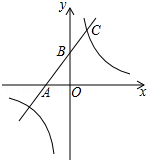 如图,一次函数的图象与x轴、y轴分别相交于A、B两点,且与反比例函数y=$\frac{k}{x}$(k≠0)的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.
如图,一次函数的图象与x轴、y轴分别相交于A、B两点,且与反比例函数y=$\frac{k}{x}$(k≠0)的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com