
【题目】如图,已知□ABCD中,DE是∠ADC的角平分线,交BC于点E . 
(1)求证:CD=CE;
(2)若BE=CE , 求证:AE⊥DE.
【答案】
(1)证明:∵ 四边形ABCD是平行四边形,
∴ AD∥BC ,
∴ ∠ADE=∠DEC.
∵ DE是∠ADC的角平分线,
∴ ∠ADE=∠CDE ,
∴ ∠CDE=∠DEC ,
∴ CD=CE
(2)证明:∵ 四边形ABCD是平行四边形,
∴ AB=DC.
∵ CD=CE , BE=CE
∴ AB=BE,
∴ ∠BAE=∠BEA.
∵ AD∥BC ,
∴ ∠DAE=∠BEA.
∴ ∠DAE=∠BAE= ![]() ∠BAD.
∠BAD.
∵ AB∥DC ,
∴ ∠BAD+∠ADC=180°,
∵ ∠ADE= ![]() ∠ADC ,
∠ADC ,
∴ ∠DAE+∠ADE= ![]() (∠BAD+∠ADC)=90°,
(∠BAD+∠ADC)=90°,
∴ ∠AED=90°,
∴ AE⊥DE.
【解析】(1)先依据角平分线的定义和平行线的性质可证明∠CDE=∠DEC,最后,依据等角对等边的性质进行证明即可;
(2)先证明BE=AB,可得到∠BAE=∠BEA,然后可证明∠BAE=∠DAE,从而可证明∠EAD+∠ADE=![]() (∠BAD+∠ADC)=90°,然后可证明∠AED=90°.
(∠BAD+∠ADC)=90°,然后可证明∠AED=90°.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在⊙O的内接四边形ACDB中,AB为直径,AC:BC=1:2,点D为![]() 的中点,BE⊥CD垂足为E.
的中点,BE⊥CD垂足为E.
(1)求∠BCE的度数;
(2)求证:D为CE的中点;

(3)连接OE交BC于点F,若AB=![]() ,求OE的长度.
,求OE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】陆地上最高处是珠穆朗玛峰的峰顶,高出海平面约8844m,记为+8844m;陆地上最低处是死海,低于海平面约415m,记为______m,珠穆朗玛峰比死海高______m;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年3月,我市某中学举行了“爱我中国朗诵比赛”活动,根据学生的成绩划分为A、B、C、D四个等级,并绘制了不完整的两种统计图.根据图中提供的信息,回答下列问题:
(1)参加朗诵比赛的学生共有 人,并把条形统计图补充完整;
(2)扇形统计图中,m= ,n= ;C等级对应扇形有圆心角为 度;
(3)学校欲从获A等级的学生中随机选取2人,参加市举办的朗诵比赛,请利用列表法或树形图法,求获A等级的小明参加市朗诵比赛的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,AD是角平分线,△ADE是等边三角形,下列结论:①AD⊥BC;②EF=FD;③BE=BD.其中正确结论的个数为( )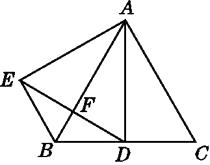
A.3
B.2
C.1
D.0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲 乙两人在相同的条件下各射靶10次,射击成绩的平均数都是8环,甲射击成绩的方差是1.2,乙射击成绩的方差是1.8.下列说法中不一定正确的是( )
A.甲、乙射击成绩的众数相同
B.甲射击成绩比乙稳定
C.乙射击成绩的波动比甲较大
D.甲、乙射中的总环数相同
查看答案和解析>>
科目:初中数学 来源: 题型:
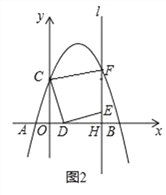
【题目】如图1,在平面直角坐标系中,抛物线y=ax2+bx+3交x轴于A(﹣1,0)和B(5,0)两点,交y轴于点C,点D是线段OB上一动点,连接CD,将线段CD绕点D顺时针旋转90°得到线段DE,过点E作直线l⊥x轴于H,交抛物线于点M,过点C作CF⊥l于F.
(1)求抛物线解析式;
(2)如图2,当点F恰好在抛物线上时(与点M重合)
①求点F的坐标;
②求线段OD的长;
③试探究在直线l上,是否存在点G,使∠EDG=45°?若存在,请直接写出点G的坐标;若不存在,请说明理由.
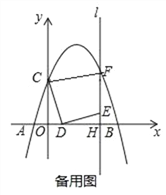
(3)在点D的运动过程中,连接CM,若△COD∽△CFM,请直接写出线段OD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com