
【题目】已知AB是⊙O的直径,AT是⊙O的切线,∠ABT=50°,BT交⊙O于点C,E是AB上一点,延长CE交⊙O于点D.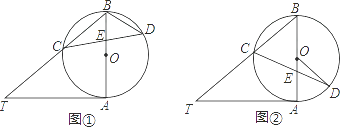
(1)如图①,求∠T和∠CDB的大小;
(2)如图②,当BE=BC时,求∠CDO的大小.
【答案】
(1)解:如图①,连接AC,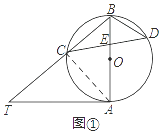
∵AT是⊙O切线,AB是⊙O的直径,
∴AT⊥AB,即∠TAB=90°,
∵∠ABT=50°,
∴∠T=90°﹣∠ABT=40°,
由AB是⊙O的直径,得∠ACB=90°,
∴∠CAB=90°﹣∠ABC=40°,
∴∠CDB=∠CAB=40°
(2)解:如图②,连接AD,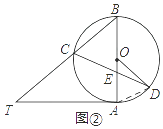
在△BCE中,BE=BC,∠EBC=50°,
∴∠BCE=∠BEC=65°,
∴∠BAD=∠BCD=65°,
∵OA=OD,
∴∠ODA=∠OAD=65°,
∵∠ADC=∠ABC=50°,
∴∠CDO=∠ODA﹣∠ADC=65°﹣50°=15°
【解析】(1)连接AC,根据圆的切线垂直于经过切点的半径可得∠TAB=90°,由已知条件可求得∠T和∠CDB的度数。
(2)连接AD,在△BCE中,根据已知条件:BE=BC,∠EBC=50°,可求得∠BCE=∠BEC=65°,由同弧所对的圆周角相等可得∠BAD=∠BCD=65°,再根据等边对等角得∠ODA=∠OAD=65°,∠CDO=∠ODA﹣∠ADC,∠CDO的度数可求。


科目:初中数学 来源: 题型:
【题目】图形的操作过程:
在图①中,将线段A1A2向右平移1个单位到B1B2 , 得到封闭图形A1A2B2B1(即阴影部分);
在图②中,将折线A1A2A3向右平移1个单位到B1B2B3 , 得到封闭图形A1A2A3B3B2B1(即阴影部分).
(1)在图③中,请你类似地画一条有两个折点的折线,同样向右平移1个单位,从而得到一个封闭图形,并用斜线画出阴影; 
(2)请你分别写出上述三个图形中除去阴影部分后剩余部分的面积:
S1= , S2= , S3= .
(3)联想与探索:
如图④在一块矩形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是1个单位),请你猜想空白部分表示的草地面积是多少并说明你的猜想是正确的.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y1=kx+b和y2=﹣4x+a的图象如图所示,且A(0,4),C(﹣2,0).
(1)由图可知,不等式kx+b>0的解集是 ;
(2)若不等式kx+b>﹣4x+a的解集是x>1.
①求点B的坐标;
②求a的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 朗读者
朗读者![]() 自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级
自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级![]() 、
、![]() 班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩
班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩![]() 满分为100分
满分为100分![]() 如图所示.
如图所示.
平均数 | 中位数 | 众数 | |
九 | 85 | 85 | |
九 | 80 |
![]() 根据图示填写表格;
根据图示填写表格;
![]() 结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
![]() 如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.
如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC, EF∥BC,∠AEF=143°,AB=AE=1.3米,那么适合该地下车库的车辆限高标志牌为多少米?(结果精确到0.1.参考数据:sin 37° ≈ 0.60,cos 37° ≈ 0.80,tan 37° ≈ 0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
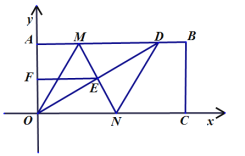
【题目】如图,在平面直角坐标系中,已知矩形AOCB的顶点O、A的坐标分别是(0,0)、(0,a),且满足![]() . 点D是AB上一点, M,N垂直平分OD,分别交AB,OD,OC于点M,E,N,连接OM,DN.
. 点D是AB上一点, M,N垂直平分OD,分别交AB,OD,OC于点M,E,N,连接OM,DN.
(1)填空:a = ;
(2)求证:四边形MOND是菱形;
(3)若F为OA的中点,连接EF,且满足EF+OE=9,求四边形MOND的周长和面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一架飞机由A向B沿水平直线方向飞行,在航线AB的正下方有两个山头C、D.飞机在A处时,测得山头C、D在飞机的前方,俯角分别为60°和30°.飞机飞行了6千米到B处时,往后测得山头C的俯角为30°,而山头D恰好在飞机的正下方.求山头C、D之间的距离.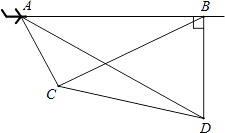
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com