
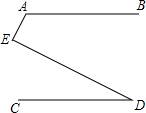
 如图所示,若AB∥CD,则∠A,∠D,∠E之间的度数关系是
如图所示,若AB∥CD,则∠A,∠D,∠E之间的度数关系是 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
 5、家住湖边的小海,帮爸爸用铁丝做网箱如图所示,若AB∥CD,AC∥BD,若∠1=α,则:①∠3=α;②∠2=180°-α;③∠4=α,其中正确的个数有( )
5、家住湖边的小海,帮爸爸用铁丝做网箱如图所示,若AB∥CD,AC∥BD,若∠1=α,则:①∠3=α;②∠2=180°-α;③∠4=α,其中正确的个数有( )查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•道里区三模)小张计划用长为6米的铝合金条制成一个矩形窗架(窗架中的横梁、竖梁皆用铝合金条制作)如图所示.若AB的长为x米,窗户的透光面积为S平方米(铝合金条所占的面积忽略不计).
(2012•道里区三模)小张计划用长为6米的铝合金条制成一个矩形窗架(窗架中的横梁、竖梁皆用铝合金条制作)如图所示.若AB的长为x米,窗户的透光面积为S平方米(铝合金条所占的面积忽略不计).| b |
| 2a |
| 4ac-b2 |
| 4a |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com