
����Ŀ���ִ������������Ĺ㷺Ӧ�ã������˿����ҵ�ĸ��ٷ�չ��С���ƻ������ѿ��һ������Ʒ�����˽��мס������ҿ�ݹ�˾�ȽϺ��ʣ���˾��ʾ�������Ʒ������1ǧ�˵ģ���ÿǧ��22Ԫ�շѣ�����1ǧ�ˣ������IJ��ְ�ÿǧ��15Ԫ�շѣ��ҹ�˾��ʾ����ÿǧ��16Ԫ�շѣ����Ӱ�װ��3Ԫ����С�������Ʒxǧ�ˣ�
��1����ֱ�д���ס������ҿ�ݹ�˾��ݸ���Ʒ�ķ���y��Ԫ����x��ǧ�ˣ�֮��ĺ�����ϵʽ��
��2��С��ѡ���ļҿ�ݹ�˾��ʡǮ��
���𰸡���1��![]() ��
��![]() ����2����
����2����![]() ��x��4ʱ��ѡ�ҿ�ݹ�˾ʡǮ����x=4��x=
��x��4ʱ��ѡ�ҿ�ݹ�˾ʡǮ����x=4��x=![]() ʱ��ѡ�ס������ҿ�ݹ�˾��ݷ�һ���ࣻ��0��x��
ʱ��ѡ�ס������ҿ�ݹ�˾��ݷ�һ���ࣻ��0��x��![]() ��x��4ʱ��ѡ��ݹ�˾ʡǮ����
��x��4ʱ��ѡ��ݹ�˾ʡǮ����
��������
�����������1�����ݡ���˾�ķ���=��+�������������ص��ۡ��ɵó�y������x�ĺ�����ϵʽ�����ݡ��ҹ�˾�ķ���=�������������+��װ���á����ɵó�y������x�ĺ�����ϵʽ��
��2����0��x��1��x��1����������ۣ��ֱ���y����y����y��=y����y����y���������x�ķ��̻�ʽ���ɵó����ۣ�
�����������1��������֪��
��0��x��1ʱ��y��=22x����1��xʱ��y��=22+15��x��1��=15x+7��y��=16x+3��
��![]() ��
��![]() ��
��
��2���ٵ�0��x��1ʱ����y����y������22x��16x+3����ã�0��x��![]() ��
��
��y��=y������22x=16x+3����ã�x=![]() ��
��
��y����y������22x��16x+3����ã�![]() ��x��1��
��x��1��
��x��1ʱ����y����y������15x+7��16x+3����ã�x��4��
��y��=y������15x+7=16x+3����ã�x=4��
��y����y������15x+7��16x+3����ã�0��x��4��
���Ͽ�֪����![]() ��x��4ʱ��ѡ�ҿ�ݹ�˾ʡǮ����x=4��x=
��x��4ʱ��ѡ�ҿ�ݹ�˾ʡǮ����x=4��x=![]() ʱ��ѡ�ס������ҿ�ݹ�˾��ݷ�һ���ࣻ��0��x��
ʱ��ѡ�ס������ҿ�ݹ�˾��ݷ�һ���ࣻ��0��x��![]() ��x��4ʱ��ѡ��ݹ�˾ʡǮ��
��x��4ʱ��ѡ��ݹ�˾ʡǮ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬��BAC�Ľ�ƽ����AD��BC�ڵ�D����AC=5��BC=12�����D��AB�ľ��룮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ABC���ܳ�Ϊ20��AB=8����õ��������ε�����Ϊ�� ����
A.8B.6C.4D.8��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��ʱ���ڣ�ij�̳�����ijƷ�Ƶ�Ůװ30�������ֳ�������������±���
���루cm�� | 155 | 160 | 165 | 170 | 175 |
������������ | 2 | 10 | 12 | 4 | 2 |
����30��Ůװ�������������λ���ֱ��ǣ� ��
A.175cm��165cm
B.165cm��165cm
C.165cm��175cm
D.165cm��170cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
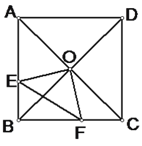
����Ŀ����������ABCD�У�O�ǶԽ��ߵĽ��㣬��O��OE��OF���ֱ�AB��BC��E��F����AE��4��CF��3��
��1����֤��OE=OF
��2���� EF�ij�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
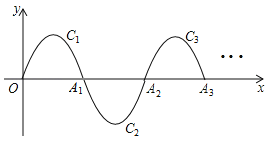
����Ŀ����ͼ��һ�������ߣ�y=��x��x��2����0��x��2����ΪC1������x�ύ������O��A1����C1��A1��ת180��õ�C2����x����A2����C2��A2��ת180��õ�C3����x����A3������˽�����ȥ��ֱ���õ�C6������P��11��m���ڵ�6��������C6�ϣ���m= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�������α���Ŀ�����������е�һ���⣺��ͼ1��ֱ��a��b���ɵĽ��ܵ���������ȥ�ˣ�����ʲô�취����������ֱ�����ɵĽǵĶ�����
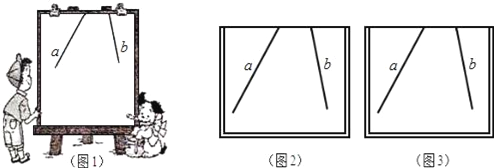
��1�������С����ͼ2�Ļ����ڻ�����IJ�������ͼ����Ҫ˵���������̣���
��˵���û������ݵĶ�����
��2��С���ڴ˻����Ͻ����˸������̽�����뵽����������
����ͼ3�Ļ����ڣ���ֱ��a��ֱ��b�ϸ�ȡһ�㣬ʹ��������ֱ��a��b�Ľ��㹹�ɵ��������Σ����н���Ϊ���ǵĶ��㣩�������õ����������ڻ����ڵIJ��֣�
����ͼ3�Ļ����ڣ�������ֱ��a��b���ɵ��ܵ���������ȥ�Ľ�����ƽ���ߣ��ڻ����ڵIJ��֣���ֻҪ������ͼ�Σ���������ͼ�ۼ���
�����С��������������������̣�������Ҫ�з���ͼ�����е��߲��ܻ��������⣬ֻ�ܻ��ڻ����ڣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������еĶ�Ӧֵ��
x | 3.24 | 3.25 | 3.26 |
ax2+bx+c | ��0.02 | 0.01 | 0.03 |
�жϹ���x�ķ���ax2+bx+c��0��a��0����һ����x�ķ�Χ�ǣ�������
A. x��3.24B. 3.24��x��3.25C. 3.25��x��3.26D. x��3.26
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�У�AB=15��AC=13����AD=12�����ABC�����Ϊ______________��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com