练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【小题1】在半径为10的圆的铁片中，要裁剪出一个直角扇形，求能裁剪出的最大的直角扇形的面积？

    【小题2】若用这个最大的直角扇形恰好围成一个圆锥，求这个圆锥的底面圆的半径？
    【小题3】能否从最大的余料③中剪出一个圆做该圆锥的底面？请说明理由．
    p;【答案】
    【小题1】50------2分 
    【小题2】------3分
    【小题3】不能------3分解析:
    p;【解析】略
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    等腰直角△ABC和⊙O如图放置，已知AB=BC=1，∠ABC=90°，⊙O的半径为1，圆心O与直线AB的距离为5．现△ABC以每秒2个单位的速度向右移动，同时△ABC的边长AB、BC又以每秒0.5个单位沿BA、BC方向增大．
    【小题1】当△ABC的边(BC边除外)与圆第一次相切时，点B移动了多少距离？
    【小题2】 若在△ABC移动的同时，⊙O也以每秒1个单位的速度向右移动，则△ABC从开始移动，到它的边与圆最后一次相切，一共经过了多少时间？
    【小题3】在⑵的条件下，是否存在某一时刻，△ABC与⊙O的公共部分等于⊙O的面积？若存在，求出恰好符合条件时两个图形移动了多少时间？若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在平面直角坐标系中，以点C（1，1）为圆心，2为半径作圆，交x轴于A．B两点，开口向下的抛物线经过点A，B，且其顶点P在⊙C上．

    【小题1】求∠ACB的大小
    【小题2】写出A，B两点的坐标
    【小题3】由圆与抛物线的对称性可知抛物线的顶点P的坐标为（1，3），求出抛物线的解析式；
    【小题4】在该抛物线上是否存在一点D点，使线段OP与CD互相平分？若存在，求出点D的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2011年九年级下学期第一次月考数学卷 题型：解答题

    如图，在平面直角坐标系中有一矩形ABCO，B点的坐标为（12，6），点C、A在坐标轴上．⊙A、⊙P的半径均为1，点P从点C开始在线段CO上以1单位/秒的速度向左运动，运动到点O处停止．与此同时，⊙A的半径每秒钟增大2个单位，当点P停止运动时，⊙A的半径也停止变化．设点P运动的时间为t秒．
    【小题1】在0＜t＜12时，设△OAP的面积为s，试求s与t的函数关系式．并求出当t为何值时，s为矩形ABCO面积的；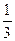
    【小题2】在点P的运动过程中，是否存在某一时刻，⊙A与⊙P相切，若存在求出点P的坐标，若不存在，说明理由．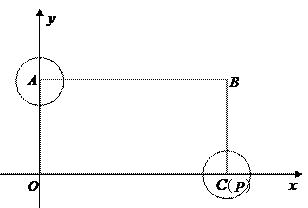

    查看答案和解析>>

    科目：初中数学 来源：2012届广东汕头澄海区中考模拟数学试卷（带解析） 题型：解答题

    在边长为1的正方形网格中，有△ABC和半径为2的⊙P．
    【小题1】以点M为位似中心，在网格中将△ABC放大2倍得到△A´B´C´，请画出△A´B´C´；

    【小题2】在(1)所画的图形中，求线段AB的对应线段A´B´被⊙P所截得的弦DE的长．

    查看答案和解析>>

    同步练习册答案