

分析 (1)第1斜列的数字的个数是1,第2斜列的数字的个数是2,第3斜列的数字的个数是3,第4斜列的数字的个数是4,…,第n斜列的数字的个数是n,根据等差数列的求和公式,求出前2012斜列的数字的个数是多少;然后根据斜列从左下角到右上角,数字逐渐增加,用前2012斜列的数字的个数加上1,求出第1列第2013行的数是多少即可.
(2)根据等差数列的求和公式,求出前n斜列的数字的个数是多少,即可判断出在第1行第n列的数是多少.
(3)根据图示,可得第1行第1列的数是1,第2行第2列的数是5=1+4,第3行第3列的数是13=5+4×2,第4行第4列的数是25=13+4×3,据此求出第5行第5列的数、第6行第6列的数是多少,进而求出位于第7行第7列的数是多少即可.
解答 解:(1)(1+2+3+…+2012)+1
=(1+2012)×2012÷2+1
=2013×2012÷2+1
=2025078+1
=2025079
所以在第1列第2013行的数是2025079.
(2)∵1+2+3+…+n=$\frac{n(n+1)}{2}$,
∴在第1行第n列的数是 $\frac{n(n+1)}{2}$.
(3)第1行第1列的数是:1,
第2行第2列的数是:5=1+4,
第3行第3列的数是:13=5+4×2,
第4行第4列的数是:25=13+4×3,
∴第5行第5列的数是:25+4×4=41,
第6行第6列的数是:41+4×5=61,
∴位于第7行第7列的数是:61+4×6=85,
即位于第7行第7列的数是85.
故答案为:2025079;$\frac{n(n+1)}{2}$.
点评 (1)此题主要考查了探寻数字规律问题,注意观察总结规律,并能正确的应用规律,解答此题的关键是判断出:①第n斜列的数字的个数是n;②斜列从左下角到右上角,数字逐渐增加.
(2)此题还考查了等差数列的求和方法:1+2+3+…+n=$\frac{n(n+1)}{2}$,要熟练掌握.


科目:初中数学 来源: 题型:选择题
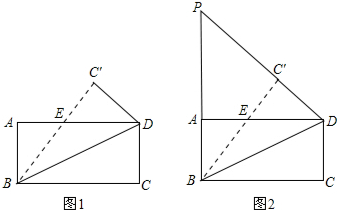
 如图,在正方形ABCD的对角线上取点E,使得∠BAE=15°,连接AE,CE,延长CE到F,连接BF,使得BC=BF.若AB=1,则下列结论:①AE=CE;②F到BC的距离为$\frac{1}{2}$;③∠AEF=60°;④图中只有三对三角形全等;⑤DE=$\frac{\sqrt{6}+\sqrt{2}}{2}$.其中正确的个数是( )
如图,在正方形ABCD的对角线上取点E,使得∠BAE=15°,连接AE,CE,延长CE到F,连接BF,使得BC=BF.若AB=1,则下列结论:①AE=CE;②F到BC的距离为$\frac{1}{2}$;③∠AEF=60°;④图中只有三对三角形全等;⑤DE=$\frac{\sqrt{6}+\sqrt{2}}{2}$.其中正确的个数是( )| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
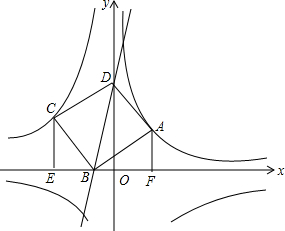 如图,点A(2,2)在双曲线y1=$\frac{k}{x}$(x>0)上,点C在双曲线y2=-$\frac{9}{x}$(x<0)上,分别过A、C向x轴作垂线,垂足分别为F、E,以A、C为顶点作正方形ABCD,且使点B在x轴上,点D在y轴的正半轴上.
如图,点A(2,2)在双曲线y1=$\frac{k}{x}$(x>0)上,点C在双曲线y2=-$\frac{9}{x}$(x<0)上,分别过A、C向x轴作垂线,垂足分别为F、E,以A、C为顶点作正方形ABCD,且使点B在x轴上,点D在y轴的正半轴上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
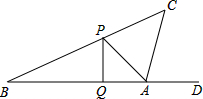 2015年 4月18日潍坊国际风筝节拉开了帷幕,这天小敏同学正在公园广场上放风筝,如图风筝从A处起飞,几分钟后便飞达C处,此时,在AQ延长线上B处的小亮同学,发现自己的位置与风筝和广场边旗杆PQ的顶点P在同一直线上.
2015年 4月18日潍坊国际风筝节拉开了帷幕,这天小敏同学正在公园广场上放风筝,如图风筝从A处起飞,几分钟后便飞达C处,此时,在AQ延长线上B处的小亮同学,发现自己的位置与风筝和广场边旗杆PQ的顶点P在同一直线上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
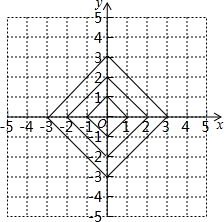 在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点,观察如图所示中每一个正方形(实践)四条边上的整点的个数,请你猜测由里向外第7个正方形(实线)四条边上的整点个数有( )
在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点,观察如图所示中每一个正方形(实践)四条边上的整点的个数,请你猜测由里向外第7个正方形(实线)四条边上的整点个数有( )| A. | 24个 | B. | 28个 | C. | 32个 | D. | 30个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com