
分析 解其中任意一对方程组,得到(2,4),再将其他代入,验证发现均经过(2,4),把(2,4)代入y=kx+5得4=2k+5,求出k的值即可.
解答 解:解法一:∵解方程组$\left\{\begin{array}{l}y=2x\\ y=-x+6\end{array}\right.$得,$\left\{\begin{array}{l}x=2\\ y=4\end{array}\right.$,
∴直线y=2x,y=-x+6过(2,4)点.
对于直线y=x+2,当x=2时,y=4;
对于直线y=4x-4,当x=2时,y=4,
∴验证发现此组直线均经过(2,4),
∴把把(2,4)代入y=kx+5得4=2k+5,得k=-$\frac{1}{2}$.
解法二:在同一直角坐标系中,正确画出y=2x,y=-x+6,y=x+2与y=4x-4其中任意的两条图象,观察它们的图象发现这些直线交于同一点(2,4)…(3分)
验证其余直线也交于同一点(2,4),把(2,4)代入y=kx+5得4=2k+5,得k=-$\frac{1}{2}$.
点评 本题考查的是一次函数的性质,熟知一次函数图象上各点的坐标均适合此函数的解析式是解答此题的关键.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:解答题
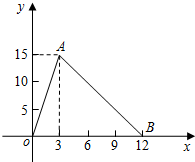 图中的折线是某类函数的图象,根据图象解答下列问题.
图中的折线是某类函数的图象,根据图象解答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 九(1)班的学生人数为40 | B. | m的值为10 | ||
| C. | n的值为20 | D. | 表示“足球”的扇形的圆心角是70° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
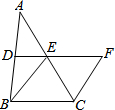 如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到F,使得EF=BE,连接CF.
如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到F,使得EF=BE,连接CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
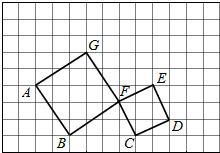 如图,建立平面直角坐标系,正方形ABFG和正方形CDEF中,使点B、C的坐标分别为(-4,0)和(0,0)
如图,建立平面直角坐标系,正方形ABFG和正方形CDEF中,使点B、C的坐标分别为(-4,0)和(0,0)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com