

���� ��1���ȸ��ݹ��ɶ������AB�����á�APC�ס�ACB���ó�$\frac{AC}{AB}=\frac{AP}{AC}$������$\frac{3\sqrt{3}}{6}=\frac{6-2t}{3\sqrt{3}}$�����ʱ�䣻
��2�����ô�ֱƽ���ߵ����ʵó�QM=CM=$\frac{1}{2}$CQ=$\frac{1}{2}$��3$\sqrt{3}$-$\sqrt{3}$t����Ȼ����ƽ���߷��߶γɱ�����������������ۣ�
��3������ƽ���ı��ε����ʽ����������ʱ��t�������PQ��PB�����ɵõ�PQ��PB�жϳ��ı���PQGB�����������Σ�
��� �⣺��1����Rt��ACB�У���C=90�㣬AC=3$\sqrt{3}$cm��BC=3cm��
��AB=6��
���˶�֪��BP=2t��AQ=$\sqrt{3}$t��
��AP=6-2t��
�ߡ�APC�ס�ACB��
��$\frac{AC}{AB}=\frac{AP}{AC}$��
��$\frac{3\sqrt{3}}{6}=\frac{6-2t}{3\sqrt{3}}$��
��t=$\frac{3}{4}$��
��2�����ڣ�
���ɣ���ͼ�ڣ����˶�֪��BP=2t��AQ=$\sqrt{3}$t��
��AP=6-2t��CQ=3$\sqrt{3}$-$\sqrt{3}$t��
�ߵ�P��CQ�Ĵ�ֱƽ�����ϣ�
��QM=CM=$\frac{1}{2}$CQ=$\frac{1}{2}$��3$\sqrt{3}$-$\sqrt{3}$t����
��AM=AQ+QM=$\sqrt{3}$t+$\frac{1}{2}$��3$\sqrt{3}$-$\sqrt{3}$t��=$\frac{3\sqrt{3}}{2}$��t+1��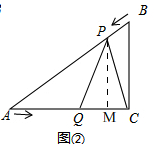 ����P��PM��AC��
����P��PM��AC��
�ߡ�ACB=90�㣬
��PM��BC��
��$\frac{AP}{AM}=\frac{BP}{CM}$��
��$\frac{6-2t}{\frac{3\sqrt{3}}{2}��t+1��}=\frac{2t}{\frac{1}{2}��3\sqrt{3}-\sqrt{3}t��}$
��t=1��t=9���ᣩ��
��t=1��
��3�������ڣ�
���ɣ����˶�֪��BP=2t��AQ=$\sqrt{3}$t��
��AP=6-2t��
�����߶�BC���Ǵ���һ��G��ʹ���ı���PQGBΪƽ���ı��Σ�
��PQ��BG��PQ=BG��
���APQ�ס�ABC��
��$\frac{AP}{AB}=\frac{AQ}{AC}=\frac{PQ}{BC}$��
��$\frac{6-2t}{6}=\frac{\sqrt{3}t}{3\sqrt{3}}=\frac{PQ}{3}$��
��t=$\frac{3}{2}$��PQ=$\frac{3}{2}$��
��BP=2t=3��
��PQ��BP��
��ƽ���ı���PQGB�����������Σ�
�����߶�BC�ϲ�����һ��G��ʹ���ı���PQGBΪ���Σ�
���� �������������ۺ��⣬��Ҫ�����˹��ɶ������߶εĴ�ֱƽ���ߵ����ʣ����������ε��ж������ʣ�ƽ���ı��ε����ʣ����ε��ж����Ȿ��Ĺؼ����÷��̵�˼�������⣮


 ����С״Ԫ��������������ϵ�д�
����С״Ԫ��������������ϵ�д� ����������ϵ�д�
����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪��ABCΪ�ȱ������Σ�BDΪ���ߣ��ӳ�BC��E��ʹCE=CD=3������DE����DE=3$\sqrt{3}$��
��֪��ABCΪ�ȱ������Σ�BDΪ���ߣ��ӳ�BC��E��ʹCE=CD=3������DE����DE=3$\sqrt{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
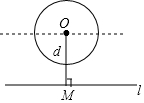 ��ͼ������һ���뾶��Ϊ2��Բ��Բ��O��ˮƽֱ��l�ľ���Ϊd����OM=d�����ǰ�Բ�ϵ�ֱ��l�ľ������1�ĵ�ĸ�����Ϊm����d=0ʱ��lΪ����Բ��O��һ��ֱ�ߣ���ʱԲ�����ĸ���ֱ��l�ľ������1�ĵ㣬��m=4���ɴ˿�֪����m=2ʱ��d��ȡֵ��Χ��1��d��3��
��ͼ������һ���뾶��Ϊ2��Բ��Բ��O��ˮƽֱ��l�ľ���Ϊd����OM=d�����ǰ�Բ�ϵ�ֱ��l�ľ������1�ĵ�ĸ�����Ϊm����d=0ʱ��lΪ����Բ��O��һ��ֱ�ߣ���ʱԲ�����ĸ���ֱ��l�ľ������1�ĵ㣬��m=4���ɴ˿�֪����m=2ʱ��d��ȡֵ��Χ��1��d��3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
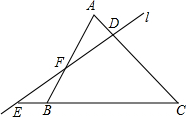 ��ͼ����ֱ֪��l�ء�ABC�������ڵ�ֱ�߷ֱ���E��F��D���㣬��AD=BE����֤��EF��FD=CA��CB��
��ͼ����ֱ֪��l�ء�ABC�������ڵ�ֱ�߷ֱ���E��F��D���㣬��AD=BE����֤��EF��FD=CA��CB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com