
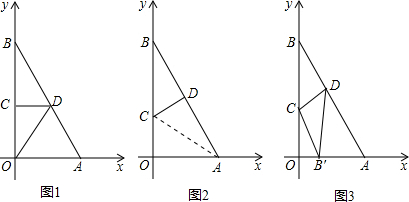
 (2)如图2,折叠后点B与点A重合,则△ACD≌△BCD,
(2)如图2,折叠后点B与点A重合,则△ACD≌△BCD,| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 8 |
| 1 |
| 8 |


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
 (2012•吴中区二模)2012年4月11曰16时38分北苏门答腊西海岸发生里氏8.6级地震,并伴有海啸.山坡上有一棵与水平面垂直的大树,海啸过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示).已知山坡的坡角∠AEF=23°,量得树干的倾斜角为∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=6m.
(2012•吴中区二模)2012年4月11曰16时38分北苏门答腊西海岸发生里氏8.6级地震,并伴有海啸.山坡上有一棵与水平面垂直的大树,海啸过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示).已知山坡的坡角∠AEF=23°,量得树干的倾斜角为∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=6m.| 2 |
| 3 |
| 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com