
【题目】如图所示,∠BAC=30°,D为角平分线上一点,DE⊥AC于E,DF∥AC,且交AB于点F.

(1)求证:△AFD为等腰三角形;
(2)若DF=10cm,求DE的长.
【答案】(1)见解析;(2)DE=5cm.
【解析】
(1)利用平行线和角平分线的性质,证得等角,利用等角对等边这一判定定理证明△AFD为等腰三角形.
(2)AD是角平分线,易证∠GFD=30°,又△GFD是直角三角形,所以30°锐角所对的直角边等于斜边的一半这一性质,求出DE=5.
(1)证明:

如图所示,
∵DF∥AC,
∴∠3=∠2,
∵AD是角平分线,
∴∠1=∠2,
∴∠1=∠3,
∴FD=FA,
∴△AFD为等腰三角形.
(2)
如图,过D作DG⊥AB,垂足为G,
∵∠1=∠2=![]() ∠BAC,∠BAC=30°,
∠BAC,∠BAC=30°,
∴∠1=15°,
又∵∠1=∠3,
∴∠1=∠3=15°,
∴∠GFD=∠1+∠3=15°+15°=30°,
在Rt△FDG中,DF=10cm,∠GFD=30°,
∴DG=5cm,
∵AD为∠BAC的平分线,DE⊥AC,DG⊥AB,
∴DE=DG=5cm.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,有一个边长不定的正方形ABCD,它的两个相对的顶点A,C分别在边长为1的正六边形一组平行的对边上,另外两个顶点B,D在正六边形内部(包括边界),则正方形边长a的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=90°,OM平分∠AOB,将直角三角板的顶点P在射线OM上移动,两直角边分别与OA、OB相交于点C、D,问PC与PD相等吗?试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 交
交![]() 轴于
轴于![]() 点,交
点,交![]() 轴于
轴于![]() 点,且
点,且![]() .点
.点![]() 是线段
是线段![]() 上一点,
上一点,![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
(1)如图1,若![]() 交
交![]() 于点
于点![]() .点
.点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,求证:
,求证:![]() ;
;

(2)如图2,若![]() 是
是![]() 的角平分线,
的角平分线,![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,求
,求![]() 的值;
的值;

(3)如图3,若![]() 交
交![]() 的延长线于点
的延长线于点![]() .请证明:
.请证明:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ADE中,∠DAE=90°,C是边AE上任意一点(点C与点A、E不重合),以AC为一直角边在Rt△ADE的外部作Rt△ABC,∠BAC=90°,连接BE、CD.
(1)在图1中,若AC=AB,AE=AD,现将图1中的Rt△ADE绕着点A顺时针旋转锐角α,得到图2,那么线段BE.CD之间有怎样的关系,写出结论,并说明理由;
(2)在图1中,若CA=3,AB=5,AE=10,AD=6,将图1中的Rt△ADE绕着点A顺时针旋转锐角α,得到图3,连接BD、CE.
①求证:△ABE∽△ACD;
②计算:BD2+CE2的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=![]() x+6与x轴,y轴相交于点A,B,点C在线段OA上,将△BOC沿着BC折叠后,点O恰好落在AB边上的点D处,若点P为平面内异于点C的一点,且满足△ABC与△ABP全等,则点P的坐标为_____.
x+6与x轴,y轴相交于点A,B,点C在线段OA上,将△BOC沿着BC折叠后,点O恰好落在AB边上的点D处,若点P为平面内异于点C的一点,且满足△ABC与△ABP全等,则点P的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
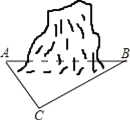
【题目】为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC距离为200m,∠CAB=54°,∠CBA=30°,求隧道AB的长.(参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38, ![]() ≈1.73,精确到个位)
≈1.73,精确到个位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(1,1),B(3,3),动点C在x轴上,若以A、B、C三点为顶点的三角形是等腰三角形,则点C的个数为( )
A.2B.3C.4D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com