
【题目】在平面直角坐标系中,直线![]() 交
交![]() 轴于
轴于![]() 点,交
点,交![]() 轴于
轴于![]() 点,且
点,且![]() .点
.点![]() 是线段
是线段![]() 上一点,
上一点,![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
(1)如图1,若![]() 交
交![]() 于点
于点![]() .点
.点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,求证:
,求证:![]() ;
;

(2)如图2,若![]() 是
是![]() 的角平分线,
的角平分线,![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,求
,求![]() 的值;
的值;

(3)如图3,若![]() 交
交![]() 的延长线于点
的延长线于点![]() .请证明:
.请证明:![]() .
.

【答案】(1)见解析;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)根据全等三角形的判定和性质即可得到结论;
(2)作BH⊥OQ交OQ的延长线于H.先证明△OAE≌△BOH,推出OE=BH,AE=OH,再证明△OED≌△BHQ,推出DE=QH,推出AD-OQ=AE+DE-(OH-HQ)=2DE,于是得到结论;
(3)如图3中,作OE平分∠AOB交AD于E.只要证明△AOE≌△OBC,推出OE=OC,再证明△ODE≌△ODC,推出∠ODE=∠ODC,由∠ODE=∠BDN,可得∠ODC=∠BDN,由此即可解决问题.
(1)证明:
∵BF⊥AD,DG⊥BF,OE∥BF,
∴∠DEA=∠OGB=90°,
∵∠OAE=∠DOE=∠OBG,OA=OB,
∴△AOE≌△BOG(AAS),
∴AE=BG;
(2)解:如图2中,作BH⊥OQ交OQ的延长线于H.
∵AD是∠OAB的角平分线,
∴∠OAD=22.5°,
∴∠ADO=67.5°,
∵AD⊥OE,
∴∠BOH=∠OAD=22.5°,
∵OA=OB,∠AEO=∠H=90°,
∴△OAE≌△BOH(AAS),
∴OE=BH,AE=OH,
∵AF⊥OH,OH⊥BH,
∴∠ADO=∠OBH=67.5°,
∵∠OBA=45°,
∴∠HBQ=∠DOE=22.5°,
∵∠OED=∠H=90°,
∴△OED≌△BHQ,
∴DE=QH,
∴AD-OQ=AE+DE-(OH-HQ)=2DE,
∴![]() .
.
(3)解:如图3中,作OE平分∠AOB交AD于E.
∵OC∥AB,
∴∠COB=∠ABO=∠AOE=45°,
∵OA=OB,∠OAE=∠OBC,
∴△AOE≌△OBC(ASA),
∴OE=OC,
∵∠EOD=∠DOC,OD=OD,
∴△ODE≌△ODC(SAS),
∴∠ODE=∠ODC,
∵∠ODE=∠BDF,
∴∠ODC=∠BDF,
∵∠CDF+∠ODC+∠BDF=180°,
∴∠CDF+2∠BDF=180°.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
【题目】节能又环保的油电混合动力汽车,既可以用油做动力行驶,也可以用电做动力行驶,某品牌油电混合动力汽车从甲地行驶到乙地,若完全用油做动力行驶,则费用为80元;若完全用电做动力行驶,则费用为30元,已知汽车行驶中每千米用油费用比用电费用多0.5元.
(1)求:汽车行驶中每千米用电费用是多少元?甲、乙两地的距离是多少千米?
(2)若汽车从甲地到乙地采用油电混合动力行驶,且所需费用不超过50元,则至少需要用电行驶多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①②,试研究其中∠1、∠2与∠3、∠4之间的数量关系;
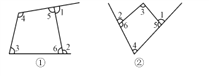
(2)如果我们把∠1、∠2称为四边形的外角,那么请你用文字描述上述的关系式;
(3)用你发现的结论解决下列问题:
如图,AE、DE分别是四边形ABCD的外角∠NAD、∠MDA的平分线,∠B+∠C=240°,求∠E的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面的内容,再解决问题.
例题:若![]() ,求
,求![]() 和
和![]() 的值.
的值.
解:∵![]()
∴![]()
即![]()
∴![]() ,
,![]()
∴![]() ,
,![]()
问题:(1)若![]() ,求
,求![]() 的值;
的值;
(2)已知![]() 是
是![]() 的三边长,满足
的三边长,满足![]() ,且
,且![]() 中最长的边的长度为
中最长的边的长度为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船以每小时40海里的速度在海面上航行,当该轮船行驶到B处时,发现灯塔C在它的东北方向,轮船继续向北航行,30分钟后到达A处,此时发现灯塔C在它的北偏东75°方向上,求此时轮船与灯塔C的距离.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠BAC=30°,D为角平分线上一点,DE⊥AC于E,DF∥AC,且交AB于点F.

(1)求证:△AFD为等腰三角形;
(2)若DF=10cm,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,CD是∠ACB的角平分线,CE是AB边上的高,
(1)若∠A=40°,∠B=60°,求∠DCE的度数.
(2)若∠A=m,∠B=n,求∠DCE.(用m、n表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,在锐角△ABC中,BD和BE三等分∠ABC,CD和CE三等分∠ACB,请分别写出∠A和∠D,∠A和∠E的数量关系,并选择其中一个说明理由;
(2)如图②,在锐角△ABC中,BD和BE三等分∠ABC,CD和CE三等分外角∠ACM,请分别写出∠A和∠D,∠A和∠E的数量关系,并选择其中一个说明理由;
(3)如图③,在锐角△ABC中,BD和BE三等分外角∠PBC,CD和CE三等分外角∠QCB,请分别直接写出∠A和∠D,∠A和∠E的数量关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com