
【题目】(1)如图①,在锐角△ABC中,BD和BE三等分∠ABC,CD和CE三等分∠ACB,请分别写出∠A和∠D,∠A和∠E的数量关系,并选择其中一个说明理由;
(2)如图②,在锐角△ABC中,BD和BE三等分∠ABC,CD和CE三等分外角∠ACM,请分别写出∠A和∠D,∠A和∠E的数量关系,并选择其中一个说明理由;
(3)如图③,在锐角△ABC中,BD和BE三等分外角∠PBC,CD和CE三等分外角∠QCB,请分别直接写出∠A和∠D,∠A和∠E的数量关系.

【答案】(1)∠A和∠D,∠A和∠E的数量关系为:∠D=60°+![]() ∠A,∠E=120°+
∠A,∠E=120°+![]() ∠A,见解析;(2)∠A和∠D,∠A和∠E的数量关系为:∠D=
∠A,见解析;(2)∠A和∠D,∠A和∠E的数量关系为:∠D=![]() ∠A,∠E=
∠A,∠E=![]() ∠A,见解析;(3)∠A和∠D,∠A和∠E的数量关系为:∠D=60°﹣
∠A,见解析;(3)∠A和∠D,∠A和∠E的数量关系为:∠D=60°﹣![]() ∠A,∠E=120°﹣
∠A,∠E=120°﹣![]() ∠A,见解析.
∠A,见解析.
【解析】
(1)利用三角形的内角和定理求出∠ABC+∠ACB,再利用三等分角求出∠EBC+∠ECB,然后列式计算即可求解;(2)根据三角形的外角等于和它不相邻的两个内角和,列式计算即可;(3)根据三角形内角和、外角和定理,及平角定义,列式计算即可.
(1)∠D=60°+![]() ∠A,∠E=120°+
∠A,∠E=120°+![]() ∠A.
∠A.
理由如下:
∵∠ABC+∠ACB=180°﹣∠A,
∵BE三等分∠ABC,CE三等分∠ACB,
∴∠EBC=![]() ∠ABC,∠ECB=
∠ABC,∠ECB=![]() ∠ACB,∠DBC=
∠ACB,∠DBC=![]() ∠ABC,∠DCB=
∠ABC,∠DCB=![]() ∠ACB,
∠ACB,
∴∠EBC+∠ECB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() (180°﹣∠A)=60°﹣
(180°﹣∠A)=60°﹣![]() ∠A,
∠A,
∠DBC+∠DCB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() (180°-∠A)=120°-
(180°-∠A)=120°-![]() ∠A,
∠A,
∴∠E=180°﹣(∠EBC+∠ECB)=180°﹣(60°﹣![]() ∠A)=120°+
∠A)=120°+![]() ∠A.
∠A.
∠D=180°-(∠DBC+∠DCB)=180°-(120°-![]() ∠A)=60°+
∠A)=60°+![]() ∠A,
∠A,
答:∠A和∠D,∠A和∠E的数量关系为:∠D=60°+![]() ∠A,∠E=120°+
∠A,∠E=120°+![]() ∠A.
∠A.
(2)∠A和∠D,∠A和∠E的数量关系为:∠D=![]() ∠A,∠E=
∠A,∠E=![]() ∠A.
∠A.
理由如下:
∵BE三等分∠ABC,CE三等分外角∠ACM,
∴∠EBC=![]() ∠ABC,∠ECM=
∠ABC,∠ECM=![]() ∠ACM,∠DBC=
∠ACM,∠DBC=![]() ∠ABC,∠DCM=
∠ABC,∠DCM=![]() ∠ACM,
∠ACM,
∴∠E=∠ECM﹣∠EBC=![]() (∠ACM﹣∠ABC)=
(∠ACM﹣∠ABC)=![]() ∠A.
∠A.
∠D=∠DCM-∠DBC=![]() (∠ACM﹣∠ABC)=
(∠ACM﹣∠ABC)=![]() ∠A.
∠A.
答:∠A和∠D,∠A和∠E的数量关系为:∠D=![]() ∠A,∠E=
∠A,∠E=![]() ∠A.
∠A.
(3)∠D=60°﹣![]() ∠A,∠E=120﹣
∠A,∠E=120﹣![]() ∠A.
∠A.
理由如下:
∵BE三等分外角∠PBC,CE三等分外角∠QCB,
∴∠CBE=![]() ∠CBP,∠BCE=
∠CBP,∠BCE=![]() ∠BCQ,∠CBD=
∠BCQ,∠CBD=![]() ∠CBP,∠BCD=
∠CBP,∠BCD=![]() ∠BCQ,
∠BCQ,
∴∠E=180°﹣![]() (∠CBP+∠BCQ)
(∠CBP+∠BCQ)
=180°﹣![]() (180°﹣∠ABC+180°﹣∠ACB)
(180°﹣∠ABC+180°﹣∠ACB)
=180°﹣120°+![]() (180°﹣∠A)
(180°﹣∠A)
=120﹣![]() A.
A.
同理:∠D=180°﹣![]() (∠CBP+∠BCQ)
(∠CBP+∠BCQ)
=180°﹣![]() (180°﹣∠ABC+180°﹣∠ACB)
(180°﹣∠ABC+180°﹣∠ACB)
=180°-120°+![]() (180°-∠A)
(180°-∠A)
=60°﹣![]() ∠A.
∠A.
答:∠A和∠D,∠A和∠E的数量关系为:∠D=60°﹣![]() ∠A,∠E=120°﹣
∠A,∠E=120°﹣![]() ∠A
∠A


科目:初中数学 来源: 题型:
【题目】某商店购进一批单价为![]() 元的日用商品,如果以单价
元的日用商品,如果以单价![]() 元销售,那么月内可售出
元销售,那么月内可售出![]() 件,根据销售经验,提高销售单价会导致销量的减少,即销售单价每提高
件,根据销售经验,提高销售单价会导致销量的减少,即销售单价每提高![]() 元,每月销售量相应减少
元,每月销售量相应减少![]() 件,请写出利润
件,请写出利润![]() 与单价
与单价![]() 之间的函数关系式________.
之间的函数关系式________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 交
交![]() 轴于
轴于![]() 点,交
点,交![]() 轴于
轴于![]() 点,且
点,且![]() .点
.点![]() 是线段
是线段![]() 上一点,
上一点,![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
(1)如图1,若![]() 交
交![]() 于点
于点![]() .点
.点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,求证:
,求证:![]() ;
;

(2)如图2,若![]() 是
是![]() 的角平分线,
的角平分线,![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,求
,求![]() 的值;
的值;

(3)如图3,若![]() 交
交![]() 的延长线于点
的延长线于点![]() .请证明:
.请证明:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=![]() x+6与x轴,y轴相交于点A,B,点C在线段OA上,将△BOC沿着BC折叠后,点O恰好落在AB边上的点D处,若点P为平面内异于点C的一点,且满足△ABC与△ABP全等,则点P的坐标为_____.
x+6与x轴,y轴相交于点A,B,点C在线段OA上,将△BOC沿着BC折叠后,点O恰好落在AB边上的点D处,若点P为平面内异于点C的一点,且满足△ABC与△ABP全等,则点P的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为﹣1、3,与y轴负半轴交于点C,在下面四个结论中:
①2a+b=0;
②c=﹣3a;
③只有当a=![]() 时,△ABD是等腰直角三角形;
时,△ABD是等腰直角三角形;
④使△ACB为等腰三角形的a的值有三个.
其中正确的结论是_____.(请把正确结论的序号都填上)

查看答案和解析>>
科目:初中数学 来源: 题型:
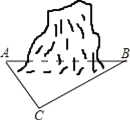
【题目】为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC距离为200m,∠CAB=54°,∠CBA=30°,求隧道AB的长.(参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38, ![]() ≈1.73,精确到个位)
≈1.73,精确到个位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰△ABC中,AB=BC=5,AC=8,点E、F分别是AC、AB上的动点,将△AEF折叠,使点A落在△ABC的边AC上点A′处(A′不与点A重合),当△A′BC为等腰三角形时,AE的长为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:


根据以上信息,整理分析数据如下:

(1)写出表格中a,b,c的值;
(2)分别运用上表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场今年2月份的营业额为400万元,3月份的营业额比2月份增加10%,5月份的营业额达到633.6万元.求3月份到5月份营业额的月平均增长率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com