
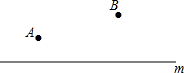 如图,某地由于居民增多,要在公路m上增加一个公共汽车站,A,B是路边两个新建小区,这个公共汽车站建在什么位置,能使两个小区到车站的路程一样长?(保留作图痕迹,不写作法)
如图,某地由于居民增多,要在公路m上增加一个公共汽车站,A,B是路边两个新建小区,这个公共汽车站建在什么位置,能使两个小区到车站的路程一样长?(保留作图痕迹,不写作法)  优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:解答题
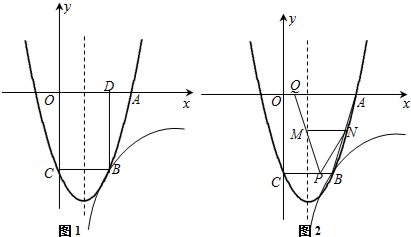
 如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.已知点C的坐标为(0,$-\frac{3}{2}$),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.
如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.已知点C的坐标为(0,$-\frac{3}{2}$),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于点A﹙-2,-5﹚C﹙5,n﹚,交y轴于点B,交x轴于点D.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于点A﹙-2,-5﹚C﹙5,n﹚,交y轴于点B,交x轴于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
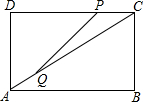 如图,在矩形ABCD中,AB=8厘米,BC=6厘米,点P从点C沿CD方向向终点D移动,同时点Q从点A沿AC方向向终点C移动,速度均为每秒1厘米,当一点到达终点时,另一点也停止运动
如图,在矩形ABCD中,AB=8厘米,BC=6厘米,点P从点C沿CD方向向终点D移动,同时点Q从点A沿AC方向向终点C移动,速度均为每秒1厘米,当一点到达终点时,另一点也停止运动查看答案和解析>>
科目:初中数学 来源: 题型:填空题
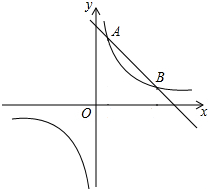 如图,直线y1=-x+b与双曲线y2=$\frac{8}{x}$交于A、B两点,点A的横坐标为1,则不等式-x+b<$\frac{8}{x}$的解集是0<x<1或x>8.
如图,直线y1=-x+b与双曲线y2=$\frac{8}{x}$交于A、B两点,点A的横坐标为1,则不等式-x+b<$\frac{8}{x}$的解集是0<x<1或x>8.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com