
���� ��1������������Եõ���a��10ʱ������������ķ��÷ֱ��Ƕ��٣�
��2�����ݵڣ�1���ʵõ��Ĵ���ʽ����a=20�ֱ���룬Ȼ���ٽ��бȽϴ�С�����ɽ���⣻
��3�����������֪������ĺ���50����100���Ӷ������Ʋ�����������
��� �⣺��1��������ɵã�
��������ķ���Ϊ��2000a��0.75=1500a��
��������ķ���Ϊ��2000����a-1����0.8=1600a-1600��
�ʴ�Ϊ��1500a��1600a-1600��
��2�������λ����֯��������Ա�����ڵĹ�20��Ա������������ѧϰ���õ�λѡ���������Ƚ��Ż�
���ɣ���a=20ʱ����������ķ���Ϊ��1500��20=30000Ԫ��
��a=20ʱ����������ķ���Ϊ��1600a-1600=1600��20-1600=32000-1600=30400��
��30000��30400��
�������λ����֯��������Ա�����ڵĹ�20��Ա������������ѧϰ���õ�λѡ���������Ƚ��Żݣ�
��3��������1��8�ų�������1��18�ų�����
���ɣ���������ĺ���50ʱ��50��5=10����1��8�ų�����
��������ĺ���100ʱ��100��5=20����1��18�ų�����
���� ���⿼���д���ʽ�ʹ���ʽ��ֵ������Ĺؼ�����ȷ���⣬�г���Ӧ�Ĵ���ʽ�������Դ���ʽ��ֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
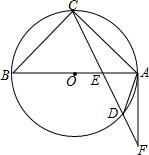 ��ͼ����֪AB�ǡ�O��ֱ������CD��AB���ڵ�E������A����O��������CD���߽��ڵ�F��AC=8��CE��ED=6��5��AE��EB=2��3����
��ͼ����֪AB�ǡ�O��ֱ������CD��AB���ڵ�E������A����O��������CD���߽��ڵ�F��AC=8��CE��ED=6��5��AE��EB=2��3�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
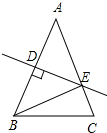 �ڡ�ABC�У�AB=AC��AB�Ĵ�ֱƽ���߽�AB�ڵ�D����AC�ڵ�E������EBC=30�㣬���A�Ķ���Ϊ��������
�ڡ�ABC�У�AB=AC��AB�Ĵ�ֱƽ���߽�AB�ڵ�D����AC�ڵ�E������EBC=30�㣬���A�Ķ���Ϊ��������| A�� | 30�� | B�� | 40�� | C�� | 50�� | D�� | 60�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | m2+��-n��2 | B�� | m2-m+1 | C�� | m2-n | D�� | m2-2m+1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
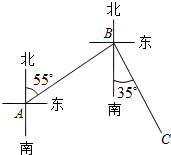 ��ͼ��ʾ��һ���˴�A����������ű�ƫ��55�㷽���ߵ�B�㣬�ٴӵ�B����������ƫ��35�㷽���ߵ�C�㣬���ABC�Ķ���Ϊ��������
��ͼ��ʾ��һ���˴�A����������ű�ƫ��55�㷽���ߵ�B�㣬�ٴӵ�B����������ƫ��35�㷽���ߵ�C�㣬���ABC�Ķ���Ϊ��������| A�� | 20�� | B�� | 90�� | C�� | 70�� | D�� | 125�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com