
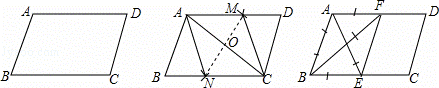
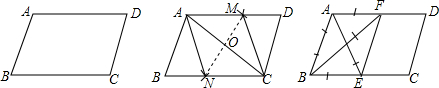
如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:
甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法可判断( )
|
| A. | 甲正确,乙错误 | B. | 乙正确,甲错误 | C. | 甲、乙均正确 | D. | 甲、乙均错误 |
考点:
菱形的判定.
分析:
首先证明△AOM≌△CON(ASA),可得MO=NO,再根据对角线互相平分的四边形是平行四边形可判定判定四边形ANCM是平行四边形,再由AC⊥MN,可根据对角线互相垂直的四边形是菱形判定出ANCM是菱形;四边形ABCD是平行四边形,可根据角平分线的定义和平行线的定义,求得AB=AF,所以四边形ABEF是菱形.
解答:
解:甲的作法正确;
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAC=∠ACN,
∵MN是AC的垂直平分线,
∴AO=CO,
在△AOM和△CON中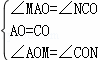 ,
,
∴△AOM≌△CON(ASA),
∴MO=NO,
∴四边形ANCM是平行四边形,
∵AC⊥MN,
∴四边形ANCM是菱形;
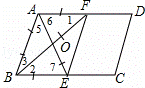
乙的作法正确;
∵AD∥BC,
∴∠1=∠2,∠6=∠7,
∵BF平分∠ABC,AE平分∠BAD,
∴∠2=∠3,∠5=∠6,
∴∠1=∠3,∠5=∠7,
∴AB=AF,AB=BE,
∴AF=BE
∵AF∥BE,且AF=BE,
∴四边形ABEF是平行四边形,
∵AB=AF,
∴平行四边形ABEF是菱形;
故选:C.
点评:
此题主要考查了菱形形的判定,关键是掌握菱形的判定方法:①菱形定义:一组邻边相等的平行四边形是菱形(平行四边形+一组邻边相等=菱形);
②四条边都相等的四边形是菱形.
③对角线互相垂直的平行四边形是菱形(或“对角线互相垂直平分的四边形是菱形”).


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(广西玉林、防城港卷)数学(解析版) 题型:选择题
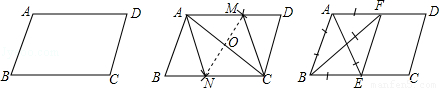
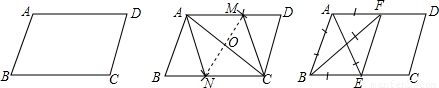
如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:
甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法可判断
A.甲正确,乙错误 B.乙正确,甲错误 C.甲、乙均正确 D.甲、乙均错误
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
查看答案和解析>>
科目:初中数学 来源:2013年广西玉林市防城港市中考数学试卷(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com