
【题目】如图是一个隧道的横断面,它的形状是以点O为圆心的圆的一部分,如果圆的半径为 ![]() m,弦CD=4m,那么隧道的最高处到CD的距离是( )
m,弦CD=4m,那么隧道的最高处到CD的距离是( ) 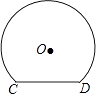
A.![]() m
m
B.4m
C.![]() m
m
D.6m
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】下表列出了国外几个城市与首都北京的时差(带正号的表示同一时刻比北京时间早的时数),如北京时间的上午10:00时,东京时间的10点已过去了1小时,现在已是10+1=11:00.
(1)如果现在是北京时间下午3:00,那么现在的纽约时间是多少?
(2)此时(北京时间9:00)小明想给远在巴黎的姑妈打电话,你认为合适吗?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为9,阴影部分三角形的面积为4.若AA'=1,则A'D等于( )

A. 2 B. 3 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛.赛后组委会整理参赛同学的成绩,并制作了如下不完整的频数分布表和频数分布直方图.
分数段(分数为x分) | 频数 | 百分比 |
60≤x<70 | 8 | 20% |
70≤x<80 | a | 30% |
80≤x≤90 | 16 | b% |
90≤x<100 | 4 | 10% |
请根据图表提供的信息,解答下列问题:
(1)表中的a= , b=;请补全频数分布直方图;
(2)若用扇形统计图来描述成绩分布情况,则分数段70≤x<80对应扇形的圆心角的度数是多少? 
查看答案和解析>>
科目:初中数学 来源: 题型:
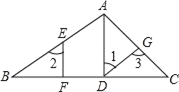
【题目】如图,在△ABC中,AD⊥BC,垂足为D,点E在AB上,EF⊥BC,垂足为F.
(1)AD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=115°,求∠BAC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把正六边形各边按同一方向延长,使延长的线段与原正六边形的边长相等,顺次连接这六条线段外端点可以得到一个新的正六边形,…,重复上述过程,经过2018次后,所得到的正六边形边长是原正六边形边长的( ) 
A.( ![]() )2016倍
)2016倍
B.( ![]() )2017倍
)2017倍
C.( ![]() )2018倍
)2018倍
D.( ![]() )2019倍
)2019倍
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AD是△ABC的中线,∠ACE是△ABC的外角. 
(1)读下列语句,尺规作图,保留作图痕迹. ①作∠ACE的角平分线,交BA延长线于点F;
②过点D作DH∥AC,交AB于点H,连接CH.
(2)依据以上条件,解答下列问题. ①与△AHD面积相等的三角形是;
②若∠B=40°,∠F=30°,求∠BAC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)如图1,在四边形ABCD中,DC∥AB,AD=BC,BD平分∠ABC.

(1)求证:AD=DC;
(2)如图2,在上述条件下,若∠A=∠ABC=60°,过点D作DE⊥AB,过点C作CF⊥BD,垂足分别为E、F,连接EF.判断△DEF的形状并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为奖励在演讲比赛中获奖的同学,班主任派学习委员小明为获奖同学买奖品,要求每人一件,小明到文具店看了商品后,决定奖品在钢笔和笔记本中选择,若买4个笔记本和2支钢笔,则需86元;若买3个笔记本和1支钢笔,则需57元.
(1)求购买一个笔记本、一支钢笔分别为多少元;
(2)售货员提示,买钢笔有优惠,具体方法是:如果买钢笔超过10支,那么超出部分可以享受8折优惠.买15支钢笔,20个笔记本,一共需要花多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com