
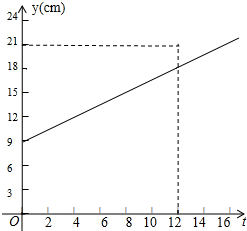
 某种植物生长t天的高度为y厘米,如图反映了y与t之间的函数关系,请根据图象回答问题:
某种植物生长t天的高度为y厘米,如图反映了y与t之间的函数关系,请根据图象回答问题:分析 (1)由图象即可确定植物刚种下时的高度;
(2)根据函数图象,即可解答;
(3)根据待定系数法求得y与t之间的函数关系式;
(4)把y=100代入函数关系式,即可解答.
解答 解:(1)植物刚种下时的高度为9cm,故答案为:9;
(2)由函数图象可得:12天后该植物高度可以达21cm,故答案为:12;
(3)设y=kx+b,
把(0,9),(12,21)代入y=kx+b得:
$\left\{\begin{array}{l}{0+b=9}\\{12k+b=21}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=1}\\{b=9}\end{array}\right.$.
故y=x+9.
(4)当y=100时,x+9=100,
解得:x=91.
答:若该植物长到100cm,需91天.
点评 本题考查了一次函数的应用,解决本题的关键是利用待定系数法求函数的解析式.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图:两条宽为a的纸条,交叉重叠放在一起,且它们的交角为α,则重叠部分的面积(阴影部分)为( )
如图:两条宽为a的纸条,交叉重叠放在一起,且它们的交角为α,则重叠部分的面积(阴影部分)为( )| A. | a2sinα | B. | a2 | C. | $\frac{{a}^{2}}{sinα}$ | D. | $\frac{{a}^{2}}{cosα}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com