
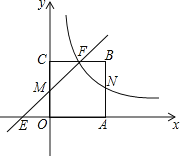
【题目】如图,已知:矩形OABC的顶点A,C分别在x,y轴的正半轴上,O为平面直角坐标系的原点;直线y=x+1分别交x,y轴及矩形OABC的BC边于E,M,F,且△EOM≌△FCM;过点F的双曲线y=![]() (x>0)与AB交于点N.
(x>0)与AB交于点N.
(1)求k的值;
(2)当x 时,![]() >x+1;
>x+1;
(3)若F为BC中点,求BN的长.
【答案】(1)2;(2)0<x<1;(3)1
【解析】
试题分析:(1)先根据一次函数的解析式求出E、M两点的坐标,再由△EOM≌△FCM得出OM=OC=1,故可得出F点的坐标,根据点F在双曲线上即可得出k的值;
(2)利用函数图象即可直接得出结论;
(3)先求出N点坐标,再由矩形的性质即可得出结论.
解:∵当x=0时,y=1;当y=0时,x=﹣1
∴OE=OM=1.
∵△EOM≌△FCM,
∴CM=CF=OE=OM=1,
∴F(1,2).
(1)∵y=![]() 的图象过点F(1,2),
的图象过点F(1,2),
∴k=1×2=2;
(2)由函数图象可知,当0<x<1时,![]() >x+1.
>x+1.
故答案为:0<x<1;
(3)∵F为矩形OABC的BC边中点,
∴B(2,2)
∴N(2,a)
∵N在y=![]() 上
上
∴a=![]() ,
,
∴a=1,
∴AN=1.
∵AB=OC=2,
∴BN=BA﹣AN=2﹣1=1.


科目:初中数学 来源: 题型:
【题目】如图,点A是⊙O上一点,OA⊥AB,且OA=1,AB=![]() ,OB交⊙O于点D,作AC⊥OB,垂足为M,并交⊙O于点C,连接BC.
,OB交⊙O于点D,作AC⊥OB,垂足为M,并交⊙O于点C,连接BC.
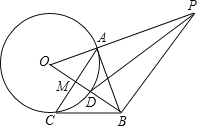
(1)求证:BC是⊙O的切线;
(2)过点B作BP⊥OB,交OA的延长线于点P,连接PD,求sin∠BPD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据国家发改委实施“阶梯水价”的有关文件要求,某市结合地方实际,决定从2016年1月1日起对居民生活用水按新的“阶梯水价”标准收费,某中学研究学习小组的同学们在社会实践活动中调查了30户家庭某月的用水量,如表所示:
用水量(吨) | 15 | 20 | 25 | 30 | 35 |
户数 | 3 | 6 | 7 | 9 | 5 |
则这30户家庭该用用水量的众数和中位数分别是( )
A.25,27 B.25,25 C.30,27 D.30,25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两超市(大型商场)同时开业,为了吸引顾客,都举行有奖酬宾活动:凡购物满100元,均可得到一次摸奖的机会.在一个纸盒里装有2个红球和2个白球,除颜色外其它都相同,摸奖者一次从中摸出两个球,根据球的颜色决定送礼金券(在他们超市使用时,与人民币等值)的多少.(如下表)
甲超市:
球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 5 | 10 | 5 |
乙超市:
球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 10 | 5 | 10 |
(1)用树状图表示得到一次摸奖机会时中礼金券的所有情况;
(2)如果只考虑中奖因素,你将会选择去哪个超市购物?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】判断题
(1)不相交的两条直线叫做平行线.( )
(2)在同一平面内,不相交的两条射线是平行线.( )
(3)如果一条直线与两条平行线中的一条平行, 那么它与另一条也互相平行.( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图在△ABC中,∠B>∠C,AD是BC边上的高,AE平分∠BAC.
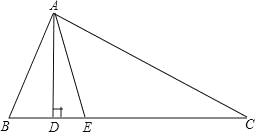
(1)若∠B=40°,∠C=30°,则∠DAE= ;
(2)若∠B=80°,∠C=40°,则∠DAE= ;
(3)由(1)、(2)我能猜想出∠DAE与∠B、∠C之间的关系为 .理由如下:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com