
【题目】如图,需在一面墙上绘制两个形状相同的抛物绒型图案,按照图中的直角坐标系,最高点M到横轴的距离是4米,到纵轴的距离是6米;纵轴上的点A到横轴的距离是1米,右侧抛物线的最大高度是左侧抛物线最大高度的一半.(结果保留整数或分数,参考数据: ![]() =
= ![]() ,
, ![]() =
= ![]() )
) 
(1)求左侧抛物线的表达式;
(2)求右侧抛物线的表达式;
(3)求这个图案在水平方向上的最大跨度是多少米.
【答案】
(1)解:最高点M到横轴的距离是4米,到纵轴的距离是6米
∴M(6,4),
设左侧抛物线的表达式为y=a(x﹣6)2+4,
把A(0,1)代入y=a(x﹣6)2+4得a=﹣ ![]() ,
,
∴左侧抛物线的表达式为y=﹣ ![]() (x﹣6)2+4
(x﹣6)2+4
(2)解:∵抛物线y=﹣ ![]() (x﹣6)2+4与x轴的交点C(13,0),
(x﹣6)2+4与x轴的交点C(13,0),
∵右侧抛物线与左侧抛物线形状相同,
∴设右侧抛物线的表达式为y=﹣ ![]() (x﹣h)2+2,
(x﹣h)2+2,
把C(13,0)代入y=﹣ ![]() (x﹣h)2+2得0=﹣
(x﹣h)2+2得0=﹣ ![]() (13﹣h)2+2,
(13﹣h)2+2,
解得:h=18,h=8(不合题意,舍去),
∴右侧抛物线的表达式为y=﹣ ![]() (x﹣18)2+2
(x﹣18)2+2
(3)解:∵C(13,0),右侧抛物线的对称轴是直线x=18,
∴D(23,0),
∴这个图案在水平方向上的最大跨度是23米
【解析】(1)根据已知条件得到M(6,4),设左侧抛物线的表达式为y=a(x﹣6)2+4,把A(0,1)代入y=a(x﹣6)2+4即可得到结论;(2)根据(1)中的结论设右侧抛物线的表达式为y=﹣ ![]() (x﹣h)2+2,把C(13,0)代入y=﹣
(x﹣h)2+2,把C(13,0)代入y=﹣ ![]() (x﹣h)2+2即可得到结论;(3)求出D(23,0),于是得到结论.
(x﹣h)2+2即可得到结论;(3)求出D(23,0),于是得到结论.


科目:初中数学 来源: 题型:
【题目】(A2013防城港)如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下: 甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法可判断( )
A.甲正确,乙错误
B.乙正确,甲错误
C.甲、乙均正确
D.甲、乙均错误
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校教学楼AB的后面有一建筑物CD,在距离CD的正后方30米的观测点P处,以22°的仰角测得建筑物的顶端C恰好挡住教学楼的顶端A,而在建筑物CD上距离地面3米高的E处,测得教学楼的顶端A的仰角为45°,求教学楼AB的高度.
(参考数据:sin22°≈ ![]() ,cos22°≈
,cos22°≈ ![]() ,tan22°≈
,tan22°≈ ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过8min时,材料温度降为600℃.煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图).已知该材料初始温度是32℃. 
(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作.那么锻造的操作时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AC⊥BC,AD⊥BD,E为AB的中点,
(1)如图1,求证:△ECD是等腰三角形;
(2)如图2,CD与AB交点为F,若AD=BD,EF=3,DE=4,求CD的长.
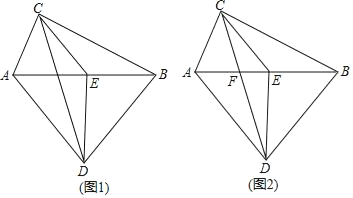
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,AB=4,BC=5,∠ABC=60°,对角线AC,BD交于点O,过点O作OE⊥AD,则OE等于( ) 
A.![]()
B.2 ![]()
C.2
D.2.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是CD的中点,AE是延长线交BC的延长线于F,分别连接AC,DF,解答下列问题: 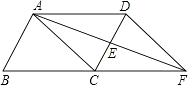
(1)求证:△ADE≌△FCE;
(2)若DC平分∠ADF,试确定四边形ACFD是什么特殊四边形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分如下表:
笔 试 | 面 试 | 体 能 | |
甲 | 85 | 80 | 75 |
乙 | 80 | 90 | 73 |
丙 | 83 | 79 | 90 |
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.
(2)该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,并按60%,30%,10%的比例计入总分(不计其他因素条件),请你说明谁将被录用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com